题目内容
19.下列命题正确的是( )| A. | 若$\underset{lim}{n→∞}$(an•bn)=a≠0,则$\underset{lim}{n→∞}$an≠0且$\underset{lim}{n→∞}$bn≠0 | |
| B. | 若$\underset{lim}{n→∞}$(an•bn)=0,则$\underset{lim}{n→∞}$an=0或$\underset{lim}{n→∞}$bn=0 | |
| C. | 若无穷数列{an}有极限,且它的前n项和为Sn,则$\underset{lim}{n→∞}{S}_{n}$=$\underset{lim}{n→∞}$a1+$\underset{lim}{n→∞}$a2+…+$\underset{lim}{n→∞}$an | |
| D. | 若无穷数列{an}有极限,则$\underset{lim}{n→∞}$an=$\underset{lim}{n→∞}$an+1 |
分析 对于A,可举an=n,bn=$\frac{1}{n}$,由数列极限的公式即可判断;对于B,可举an=n,bn=$\frac{1}{{n}^{2}}$,运用数列极限的公式即可判断;对于C,可举an=($\frac{1}{2}$)n-1,Sn=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$,求出极限即可判断;对于D,可举an=$\frac{1}{n}$,求出极限,结合n,n+1趋向于无穷,即可判断.
解答 解:对于A,若$\underset{lim}{n→∞}$(an•bn)=a≠0,可举an=n,bn=$\frac{1}{n}$,
即有$\underset{lim}{n→∞}$an不存在,$\underset{lim}{n→∞}$$\frac{1}{n}$=0,故A错;
对于B,若$\underset{lim}{n→∞}$(an•bn)=0,可举an=n,bn=$\frac{1}{{n}^{2}}$,则$\underset{lim}{n→∞}$an不存在,$\underset{lim}{n→∞}$bn=0,故B错;
对于C,若无穷数列{an}有极限,且它的前n项和为Sn,可举an=($\frac{1}{2}$)n-1,Sn=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$,
即有$\underset{lim}{n→∞}$an=0,$\underset{lim}{n→∞}$Sn=2,显然$\underset{lim}{n→∞}{S}_{n}$=$\underset{lim}{n→∞}$a1+$\underset{lim}{n→∞}$a2+…+$\underset{lim}{n→∞}$an不成立,故C错;
对于D,若无穷数列{an}有极限,可举an=$\frac{1}{n}$,$\underset{lim}{n→∞}$$\frac{1}{n}$=0,显然$\underset{lim}{n→∞}$$\frac{1}{n+1}$=0,故D正确.
故选:D.
点评 本题考查数列极限的运算性质的运用,考查命题正确与否的判断方法:列举法,考查推理能力,属于基础题和易错题.

 阅读快车系列答案
阅读快车系列答案| A. | -$\frac{7}{5}$ | B. | -$\frac{11}{5}$ | C. | $\frac{11}{5}$ | D. | $\frac{7}{5}$ |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 以上都不对 |
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 4 | D. | 1 |
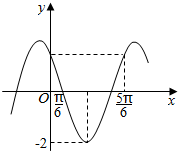 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)的部分图象如图所示,且f(0)=f($\frac{5π}{6}$).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)的部分图象如图所示,且f(0)=f($\frac{5π}{6}$).