在一圆上任取3点.这三点为顶点的三角形为钝角三角形的概率是( )A．$\frac{1}{4}$B．$\frac{1}{2}$C．$\frac{3}{4}$D．以上都不对题目和参考答案——青夏教育精英家教网—

题目内容

4．在一圆上任取3点，这三点为顶点的三角形为钝角三角形的概率是（　　）

A．

$\frac{1}{4}$

B．

$\frac{1}{2}$

C．

$\frac{3}{4}$

D．

以上都不对

分析根据题意，将圆周按逆时针方向依次标记三点为A、B、C，设出弧AB、弧BC与弧CA的长度，得到所有可能的结果构成的平面区域与“三点组成锐角三角形”构成的平面区域，分别算出两个区域的面积再利用几何概型公式加以计算，可得能构成锐角或直角三角形的概率，即可得出结论．

解答解：如图①，设半径为1，按逆时针方向依次标记三点为A、B、C，设弧AB=x，弧BC=y，弧CA=2π-x-y．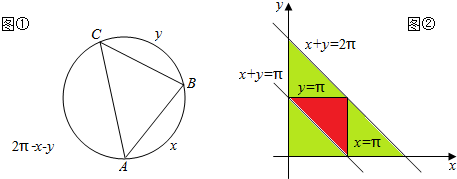

依题意，所有可能的结果构成平面区域为：Ω={（x，y）|0＜x＜2π，0＜y＜2π，0＜2π-x-y＜2π}．
事件A=“三点组成锐角或直角三角形”构成的平面区域为：A={（x，y）∈Ω|0＜x≤π，0＜y＜π，0＜2π-x-y＜π}．
分别作出Ω与A中不等式组对应的平面区域，得到两个三角形及其内部区域，如图②所示
∵平面区域Ω的面积为2π²，平面区域A的面积为$\frac{1}{2}×π×π$=$\frac{1}{2}{π}^{2}$，
∴故所求概率为P（A）=$\frac{1}{4}$．
∴在一圆上任取3点，这三点为顶点的三角形为钝角三角形的概率是1-$\frac{1}{4}$=$\frac{3}{4}$．
故选：C．

点评本题给出圆周上的任意三点，求此三点能构成钝角三角形的概率，着重考查了圆内接三角形、二元一次不等式组表示的平面区域和几何概型计算公式等知识，属于中档题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

14．设f（x）=xlnx+2015，若f′（x₀）=2，则x₀=（　　）

e²

15．若x，y满足约束条件$\left\{\begin{array}{l}{x-3y+1≤0}\\{x+y-3≤0}\\{x-1≥0}\end{array}\right.$，则z=y-x的最大值为（　　）

12．某同学用五点法画函数$f（x）=Asin（ωx+φ），（ω＞0，|φ|＜\frac{π}{2}）$在某一个周期内的图象时，列表并填入了部分数据，如表：

ωx+φ	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
x		$\frac{π}{3}$		$\frac{5π}{6}$
Asin（ωx+φ）	0	3		-3	0

（Ⅰ）请将表数据补充完整，并直接写出函数f（x）的解析式；
（Ⅱ）若函数f（x）的单调递增区间；
（Ⅲ）求f（x）在区间$[-\frac{π}{4}\;，\;\frac{π}{6}]$上的最小值．

19．下列命题正确的是（　　）

	A．	若$\underset{lim}{n→∞}$（a_n•b_n）=a≠0，则$\underset{lim}{n→∞}$a_n≠0且$\underset{lim}{n→∞}$b_n≠0
	B．	若$\underset{lim}{n→∞}$（a_n•b_n）=0，则$\underset{lim}{n→∞}$a_n=0或$\underset{lim}{n→∞}$b_n=0
	C．	若无穷数列{a_n}有极限，且它的前n项和为S_n，则$\underset{lim}{n→∞}{S}_{n}$=$\underset{lim}{n→∞}$a₁+$\underset{lim}{n→∞}$a₂+…+$\underset{lim}{n→∞}$a_n
	D．	若无穷数列{a_n}有极限，则$\underset{lim}{n→∞}$a_n=$\underset{lim}{n→∞}$a_n+1