题目内容
6.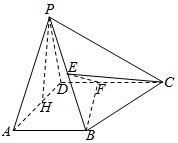 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=$\frac{1}{2}$AB,PH为△PAD中AD边上的高.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=$\frac{1}{2}$AB,PH为△PAD中AD边上的高.(Ⅰ)证明:EF⊥平面PAB;
(Ⅱ)若PH=3,AD=$\sqrt{3}$,FC=1,求三棱锥E-BCF的体积.
分析 (I)取PA中点G,连结DG,FG.则FG$\stackrel{∥}{=}$DF,故四边形EFDG是平行四边形,于是DG∥EF,将问题转化为证明DG⊥平面PAB即可;
(II)由AB⊥平面PAB得AB⊥AD,AB⊥PH,故而PH⊥平面ABCD,AD⊥CD,于是E到底面ABCD的距离为$\frac{1}{2}PH$,代入棱锥的体积公式计算即可.
解答  证明:(I)取PA中点G,连结DG,FG.
证明:(I)取PA中点G,连结DG,FG.
∵E,G是PB,PA的中点,
∴FG$\stackrel{∥}{=}$$\frac{1}{2}AB$,
又∵DF$\stackrel{∥}{=}\frac{1}{2}AB$,
∴FG$\stackrel{∥}{=}$DF,
∴四边形EFDG是平行四边形,
∴DG∥EF.
∵AB⊥平面PAD,DG?平面PAD,
∴AB⊥DG,
∵AD=PD,G是PA的中点,
∴DG⊥PA,
又PA?平面PAB,AB?平面PAB,PA∩AB=A,
∴DG⊥平面PAB,∵DG∥EF,
∴EF⊥平面PAB.
解:(II)∵AB⊥平面PAD,PH?平面PAD,AD?平面PAD,
∴AB⊥PH,AB⊥AD,
又AB∥CD,PH⊥AD,
∴PH⊥平面ABCD,S△BCF=$\frac{1}{2}FC•AD$=$\frac{\sqrt{3}}{2}$.
∵E是PB的中点,
∴E到平面ABCD的距离h=$\frac{1}{2}PH$=$\frac{3}{2}$.
∴VE-BFC=$\frac{1}{3}$S△BCF•h=$\frac{1}{3}×\frac{\sqrt{3}}{2}×\frac{3}{2}$=$\frac{\sqrt{3}}{4}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
16.设O为坐标原点,F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的焦点,若在双曲线上存在点M,满足∠F1MF2=60°,|OM|=2a,则该双曲线的渐近线方程为( )
| A. | x±2y=0 | B. | 2x±y=0 | C. | x±y=0 | D. | $\sqrt{2}x±y=0$ |
14.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)的右焦点F,且斜率为2的直线l与双曲线的相交于点A,B,若弦AB的中点横坐标取值范围为(2c,4c),则该双曲线的离心率的取值范围是( )
| A. | (3,4) | B. | (2,3) | C. | $(\sqrt{3},4)$ | D. | $(\sqrt{3},2)$ |
18.过原点的直线l与双曲线$\frac{x^2}{9}-\frac{y^2}{3}=-1$有两个交点,则直线l的倾斜角的取值范围是( )
| A. | $[{\frac{π}{6},\frac{5π}{6}}]$ | B. | $({\frac{π}{6},\frac{5π}{6}})$ | C. | $({\frac{π}{6},\frac{π}{2}})∪({\frac{π}{2},\frac{5π}{6}})$ | D. | $[{\frac{π}{6},\frac{π}{2}})∪({\frac{π}{2},\frac{5π}{6}}]$ |
16.将4本完全相同的小说,1本诗集全部分给4名同学,每名同学至少1本书,则不同分法有( )
| A. | 24种 | B. | 28种 | C. | 32种 | D. | 16种 |
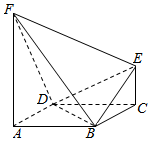 如图,在几何体ABCDEF中,FA⊥平面ABCD,EC∥FA,FA=2EC=2$\sqrt{2}$,底面ABCD为平行四边形,AD⊥BD,AD=BD=2,FD⊥BE.
如图,在几何体ABCDEF中,FA⊥平面ABCD,EC∥FA,FA=2EC=2$\sqrt{2}$,底面ABCD为平行四边形,AD⊥BD,AD=BD=2,FD⊥BE.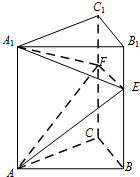 如图,正三棱柱ABC-A1B1C1中,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,则三棱锥A-A1EF的体积是8$\sqrt{3}$.
如图,正三棱柱ABC-A1B1C1中,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,则三棱锥A-A1EF的体积是8$\sqrt{3}$.