题目内容
10．$\overrightarrow{CB}+\overrightarrow{AD}-\overrightarrow{AB}$=$\overrightarrow{CD}$．分析 根据向量的加减的几何意义即可求出
解答 解：$\overrightarrow{CB}+\overrightarrow{AD}-\overrightarrow{AB}$=$\overrightarrow{CB}$+$\overrightarrow{BA}$+$\overrightarrow{AD}$=$\overrightarrow{CD}$，
故答案为：$\overrightarrow{CD}$．
点评 本题考查了向量的加减的几何意义，属于基础题．
练习册系列答案
相关题目
1．已知Rt△ABC中，AB=3，AC=1，$∠A=\frac{π}{2}$，以B，C为焦点的双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）经过点A，且与AB边交于点D，若$\frac{{|{AD}|}}{{|{BD}|}}$的值为（ ）
| A． | $\frac{7}{2}$ | B． | 3 | C． | $\frac{9}{2}$ | D． | 4 |
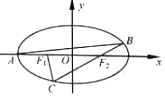如图，设点A，F1，F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左，右焦点，过点A作斜率为k的直线交椭圆于另一点B，连接BF2并延长交椭圆于点C．
5．不等式-$\frac{x-1}{x+2}$＞-|$\frac{x-1}{x+2}$|的解集为（ ）
| A． | （-∞，-2）∪（1，+∞） | B． | （-∞，-2） | C． | （1，+∞） | D． | （-2，1） |