题目内容
已知a∈[0,3],b∈[0,3],则直线ax+by+2=0与圆x2+y2=1有公共点的概率为 .
考点:几何概型
专题:应用题,概率与统计
分析:利用直线和圆有公共点,得到a,b满足的条件,利用几何概型的概率公式求出对应的面积即可得到结论.
解答:
解;∵a,b是区间[0,3]上的两个随机数,
∴a,b对应区域面积为3×3=9,
若直线ax+by+2=0与圆x2+y2=1有公共点,
则原点到直线的距离d=
≤1,
即a2+b2≥4,对应的区域为半径为2的圆及其外部部分,
则根据几何概型的概率公式可得所求的概率为P=1-
=1-
,
故答案为:1-
.
∴a,b对应区域面积为3×3=9,
若直线ax+by+2=0与圆x2+y2=1有公共点,
则原点到直线的距离d=
| 2 | ||
|
即a2+b2≥4,对应的区域为半径为2的圆及其外部部分,
则根据几何概型的概率公式可得所求的概率为P=1-
| ||
| 9 |
| π |
| 9 |
故答案为:1-
| π |
| 9 |
点评:本题主要考查几何概型的概率计算,根据直线与圆的位置关系求出a,b满足的条件是解决本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
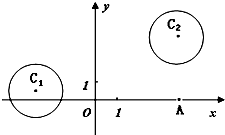 如图:已知圆C1:(x+3)2+(y-1)2=4与圆C2:(x-4)2+(y-5)2=4.
如图:已知圆C1:(x+3)2+(y-1)2=4与圆C2:(x-4)2+(y-5)2=4.