题目内容
在极坐标系中,圆ρ=6cosθ+2
sinθ(ρ>0,0≤θ<2π),则圆心的极坐标是 .
| 3 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把圆的极坐标方程化为直角坐标方程,求出圆心的直角坐标,再化为极坐标.
解答:
解:圆ρ=6cosθ+2
sinθ(ρ>0,0≤θ<2π),即ρ2=6ρcosθ+2
ρsinθ,
化为直角坐标方程为 (x-3)2+(y-
)2=12,
故它的圆心的直角坐标为(3,
),化为极坐标为 (2
,
),
故答案为:(2
,
).
| 3 |
| 3 |
化为直角坐标方程为 (x-3)2+(y-
| 3 |
故它的圆心的直角坐标为(3,
| 3 |
| 3 |
| π |
| 6 |
故答案为:(2
| 3 |
| π |
| 6 |
点评:本题主要考查曲线的极坐标方程与曲线的直角坐标方程的互化,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
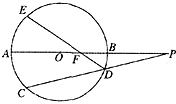 已知⊙O的半径R=2,P为直径AB延长线上一点,PB=3,割线PDC交⊙O于D,C两点,E为⊙O上一点,且
已知⊙O的半径R=2,P为直径AB延长线上一点,PB=3,割线PDC交⊙O于D,C两点,E为⊙O上一点,且