题目内容

1554与2405的最大公约数是（　　）
A、37B、39
C、111D、243
考点：辗转相除法
专题：算法和程序框图
分析：利用两个数中较大的一个除以较小的数字，得到商是a，余数是b，用1554除以b，得到商是c，依此类推，没有余数，所以两个数字的最大公约数是37，得到结果．
解答： 解：∵2405÷1554=1…851，
1554÷851=1…703，
851÷703=1…148，
703÷148=4…111，
148÷111=1…37
111÷37=3
∴1554与2405的最大公约数是37，
故选：A．
点评：本题考查用辗转相除计算最大公约数，是一个基础题，这种题目出现的概率不多，属于基础题．
练习册系列答案
相关题目
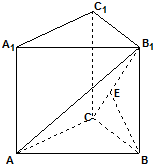如图，在直三棱柱A1B1C1-ABC中，侧面ABB1A1是边长为2的正方形，直角三角形边满足AC=BC，E是CB1上的点，且BE⊥平面ACB1．
（Ⅰ）求证：AC⊥平面BB1C；
（Ⅱ）求二面角B-AB1-C的平面角的余弦值．
若f（x）是R上的奇函数，在[0，+∞）上图象如图所示，则满足f（x-1）＞0的x的集合是
 
．
如图的程序运行后，输出a的值是（　　）
A、8B、7C、6D、4
解不等式：-1＜ln（2x-1）＜1．
已知f（x）对一切实数x，y都有f（x+y）=f（x）+f（y），f（1）=-2，当x＞0时，f（x）＜0．
（1）证明f（x）为R上的减函数；
（2）解不等式f（x-1）-f（1-2x-x2）＜4．
已知x
3
8
=2
3
4
，则x=
 
．
已知函数f（x+1）是定义在R上的奇函数，若对于任意给定的不等实数x1，x2，不等式（x1-x2）[f（x1）-f（x2）]＜0恒成立，则f（x2-
3
2
x）＜0的解集为
 
．
已知函数f（2x-1）的定义域为（1，2），则函数f（x+1）的定义域为（　　）
A、（0，2）
B、（1，2）
C、（1，3）
D、（0，3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网