题目内容
在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为:ρsin2θ=cosθ.
(1)求曲线C的直角坐标方程;
(2)若直线L的参数方程为
(t为参数),直线L与曲线C相交于A、B两点,求|AB|.
(1)求曲线C的直角坐标方程;
(2)若直线L的参数方程为
|
考点:直线的参数方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)利用公式
化简ρ2sin2θ=ρcosθ,得到曲线C的直角坐标方程;
(2)把直线的参数方程代入曲线C的普通方程中,得到方程t2+
t-4=0;
由根与系数的关系得t1+t2,t1t2,求出|AB|=|t1-t2|.
|
(2)把直线的参数方程代入曲线C的普通方程中,得到方程t2+
| 2 |
由根与系数的关系得t1+t2,t1t2,求出|AB|=|t1-t2|.
解答:
解:(1)把
代入ρ2sin2θ=ρcosθ中,
化简,得y2=x,
∴曲线C的直角坐标方程为y2=x;
(2)把
代入曲线C的普通方程y2=x中,
整理得,t2+
t-4=0,且△>0总成立;
设A、B两点对应的参数分别为t1、t2,
∵t1+t2=-
,t1t2=-4,
∴|AB|=|t1-t2|=
=3
.
|
化简,得y2=x,
∴曲线C的直角坐标方程为y2=x;
(2)把
|
整理得,t2+
| 2 |
设A、B两点对应的参数分别为t1、t2,
∵t1+t2=-
| 2 |
∴|AB|=|t1-t2|=
(-
|
| 2 |
点评:本题考查了参数方程与极坐标的应用问题,解题时应把参数方程与极坐标化为普通方程,再进行解答,是基础题.

练习册系列答案
相关题目
(x-1)5的展开式中,x3的系数为 ( )
| A、-10 | B、-5 | C、5 | D、10 |
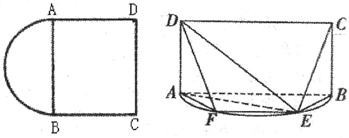
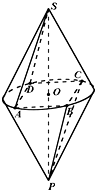 如图两个共底面的相同的圆锥,底面圆心为O,顶点分别为S和P,四边形ABCD是圆O的内接矩形,连接SA,SD,PC,PB
如图两个共底面的相同的圆锥,底面圆心为O,顶点分别为S和P,四边形ABCD是圆O的内接矩形,连接SA,SD,PC,PB
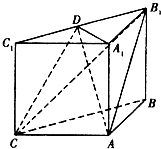 如图,三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AC=AB=AA1=4,∠BAC=90°,点D是棱B1C1的中点.
如图,三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AC=AB=AA1=4,∠BAC=90°,点D是棱B1C1的中点.