题目内容

函数f（x）=tan（2πx+
π
6
）的定义域是
 
．
考点：正切函数的定义域
专题：三角函数的图像与性质
分析：根据正切函数的定义域得：2πx+
π
6
≠
π
2
+kπ(k∈Z)，即可得到函数f（x）的定义域．
解答： 解：要是函数f（x）=tan（2πx+
π
6
）有意义，
则2πx+
π
6
≠
π
2
+kπ(k∈Z)，解得x≠
1
6
+
k
2
，k∈Z，
所以函数f（x）的定义域是{x|x≠
1
6
+
k
2
，k∈Z}，
故答案为：{x|x≠
1
6
+
k
2
，k∈Z}．
点评：本题考查了正切函数的定义域，属于基础题．
练习册系列答案
相关题目
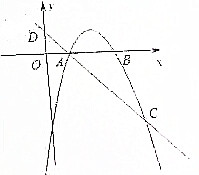如图，已知抛物线y=ax2+bx-3（a≠0）与x轴交于A，B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，-3）．
（1）求抛物线解析式；
（2）点M是（1）中抛物线上一个动点，且位于直线AC的上方，试求△ACM的最大面积以及此时点M的坐标；
（3）抛物线上是否存在点P，使得△PAC是以AC为直角边的直角三角形？如果存在，求出P点的坐标；如果不存在，请说明理由．
已知f（x）是奇函数，且有f（x+1）=-
1
f(x)
，当x∈（0，
1
2
）时，f（x）=8x，
（1）求f（-
1
3
），f（
2
3
），f（
5
3
）的值；
（2）当
1
2
＜x＜1时，求f（x）的解析式；并求证T=2为函数f（x）的一个周期；
（3）是否存在k∈N*，使2k+
1
2
＜x＜2k+1时，不等式log8f（x）＞x2-（k+3）x-k+2有解？若存在，求出k的值及对应的不等式的解；若不存在，请说明理由．
已知函数y=sin（
π
3
-2x），求：
（1）函数的周期；
（2）函数在[-π，0]上的单调递减区间．
函数f（x）=x2+bx+c，f（4）=15，f（3）+f（2）+1=0，求f（x）的图象的对称轴方程．
已知向量
a
，
b
满足|
a
|=4，且|
a
+
b
|=|
a
-
b
|=5，求|
b
|．
已知函数f（x）=lg（x+1），若g（x）满足g（x+1）=-g（x），且当0≤x≤1时，有g（x）=f（x），求函数y=g（x）（-2≤x≤-1）的解析式．
求函数f（x）=
x2-2x+2
-
x2+2x+2
的值域．
如图，四棱锥P-ABCD中，ABCD为矩形，△PAD为等腰直角三角形，∠APD=90°，平面PAD⊥平面ABCD，AB=1，AD=2，E，F分别是PC和BD的中点．
（1）证明：EF∥面PAD；    
（2）证明：面PDC⊥面PAD；
（3）求四棱锥P-ABCD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网