题目内容
已知扇形的周长为8cm.
(1)若该扇形的圆心角为2rad,求该扇形的面积.
(2)求该扇形的面积的最大值,并指出对应的圆心角.
(1)若该扇形的圆心角为2rad,求该扇形的面积.
(2)求该扇形的面积的最大值,并指出对应的圆心角.
考点:扇形面积公式
专题:综合题,三角函数的求值
分析:(1)利用扇形的周长为8cm,弧长公式,求出r,l,即可求该扇形的面积.
(2)由2r+l=8得l=8-2r,r∈(0,4),考得面积,利用配方法,即可求该扇形的面积的最大值,对应的圆心角.
(2)由2r+l=8得l=8-2r,r∈(0,4),考得面积,利用配方法,即可求该扇形的面积的最大值,对应的圆心角.
解答:
解:(1)设扇形的半径为r,弧长为l,圆心角为α,扇形面积为S
由题意得:2r+l=8,l=|α|r,--------------------------------------(3分)
解得r=2,l=4,--------------------------------------(5分)
S=
rl=4cm2--------------------------------------(7分)
(2)由2r+l=8得l=8-2r,r∈(0,4),--------------------------------------(9分)
则S=
rl=
r(8-2r)=4r-r2=-(r-2)2+4-------------------(11分)
当r=2时,Smax=4,此时l=4,α=
=2-------------------(13分)
由题意得:2r+l=8,l=|α|r,--------------------------------------(3分)
解得r=2,l=4,--------------------------------------(5分)
S=
| 1 |
| 2 |
(2)由2r+l=8得l=8-2r,r∈(0,4),--------------------------------------(9分)
则S=
| 1 |
| 2 |
| 1 |
| 2 |
当r=2时,Smax=4,此时l=4,α=
| l |
| r |
点评:本题考查扇形的弧长、面积公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知某线性规划问题的约束条件是
,则下列目标函数中,在点(3,1)处取得最小值得是( )
|
| A、z=2x-y | ||
| B、z=2x+y | ||
C、z=-
| ||
| D、z=-2x+y |
若关于x的方程log
x=
在区间(
,
)上有解,则实数m的取值范围是( )
| 1 |
| 2 |
| m |
| 1-m |
| 1 |
| 4 |
| 1 |
| 2 |
A、(
| ||||
B、(
| ||||
C、(-∞,
| ||||
D、(-∞,
|
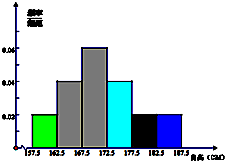 云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的平均身高为170.5cm.现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],
云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的平均身高为170.5cm.现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],