题目内容
平面上有两点A(-1,0),B(1,0),P为圆x2+y2-6x-8y+21=0上的一点,试求S=|AP|2+|BP|2的最大值与最小值,并求相应的P点坐标.
解:把已知圆的一般方程化为标准方程得(x-3)2+(y-4)2=4,设点P的坐标为(x0,y0),
则 .…(2分)
.…(2分)
∵点P(x0,y0)在已知圆上,∴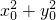 =6x0 +8y0-21=0,∴S=4(3x0 +4y0-10).
=6x0 +8y0-21=0,∴S=4(3x0 +4y0-10).
∵(x-3)2+(y-4)2=4,可设x0=3+2cosθ,y0 =4+2sinθ.
∴S=4(3x0 +4y0-10)=4(6cosθ+8sinθ+15)=40sin(θ+∅)+60,其中,tan∅= ,0<∅<
,0<∅< .
.
∵-1≤sin(θ+∅)≤1,∴20≤S≤100,再由tan∅= ,0<∅<
,0<∅< ,可得 cos∅=
,可得 cos∅= ,sin∅=
,sin∅= .
.
当S=100时,sin(θ+∅)=1,θ+∅= ,θ=
,θ= -∅.
-∅.
∴sinθ=cos∅= ,cosθ=sin∅=
,cosθ=sin∅= ,∴x0=3+2cosθ=
,∴x0=3+2cosθ=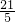 ,y0 =4+2sinθ=
,y0 =4+2sinθ=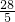 .
.
当 S=20时,sin(θ+∅)=-1,θ+∅= ,θ=
,θ= -∅.sinθ=-cos∅=-
-∅.sinθ=-cos∅=- ,cosθ=-sin∅=-
,cosθ=-sin∅=- ,
,
∴x0=3+2cosθ= y0 =4+2sinθ=
y0 =4+2sinθ= .
.
∴S的最大值是100,这时点P的坐标是 ,S的最小值是20,这时点P的坐标是(
,S的最小值是20,这时点P的坐标是( ).
).
分析:设点P的坐标为(x0,y0),则有S=4(3x0 +4y0-10),设x0=3+2cosθ,y0 =4+2sinθ,则S=40sin(θ+∅)+60,其中,tan∅= ,0<∅<
,0<∅< .根据-1≤sin(θ+∅)≤1,可得
.根据-1≤sin(θ+∅)≤1,可得
20≤S≤100,当S=100时,sin(θ+∅)=1,θ+∅= ,θ=
,θ= -∅,求出点P的坐标;同理求得 S=20时点P的坐标.
-∅,求出点P的坐标;同理求得 S=20时点P的坐标.
点评:本题主要考查正弦函数的定义域和值域,点与圆的位置关系,诱导公式的应用,属于中档题.
则
 .…(2分)
.…(2分)∵点P(x0,y0)在已知圆上,∴
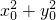 =6x0 +8y0-21=0,∴S=4(3x0 +4y0-10).
=6x0 +8y0-21=0,∴S=4(3x0 +4y0-10).∵(x-3)2+(y-4)2=4,可设x0=3+2cosθ,y0 =4+2sinθ.
∴S=4(3x0 +4y0-10)=4(6cosθ+8sinθ+15)=40sin(θ+∅)+60,其中,tan∅=
 ,0<∅<
,0<∅< .
.∵-1≤sin(θ+∅)≤1,∴20≤S≤100,再由tan∅=
 ,0<∅<
,0<∅< ,可得 cos∅=
,可得 cos∅= ,sin∅=
,sin∅= .
.当S=100时,sin(θ+∅)=1,θ+∅=
 ,θ=
,θ= -∅.
-∅.∴sinθ=cos∅=
 ,cosθ=sin∅=
,cosθ=sin∅= ,∴x0=3+2cosθ=
,∴x0=3+2cosθ=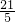 ,y0 =4+2sinθ=
,y0 =4+2sinθ=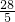 .
.当 S=20时,sin(θ+∅)=-1,θ+∅=
 ,θ=
,θ= -∅.sinθ=-cos∅=-
-∅.sinθ=-cos∅=- ,cosθ=-sin∅=-
,cosθ=-sin∅=- ,
,∴x0=3+2cosθ=
 y0 =4+2sinθ=
y0 =4+2sinθ= .
.∴S的最大值是100,这时点P的坐标是
 ,S的最小值是20,这时点P的坐标是(
,S的最小值是20,这时点P的坐标是( ).
).分析:设点P的坐标为(x0,y0),则有S=4(3x0 +4y0-10),设x0=3+2cosθ,y0 =4+2sinθ,则S=40sin(θ+∅)+60,其中,tan∅=
 ,0<∅<
,0<∅< .根据-1≤sin(θ+∅)≤1,可得
.根据-1≤sin(θ+∅)≤1,可得20≤S≤100,当S=100时,sin(θ+∅)=1,θ+∅=
 ,θ=
,θ= -∅,求出点P的坐标;同理求得 S=20时点P的坐标.
-∅,求出点P的坐标;同理求得 S=20时点P的坐标.点评:本题主要考查正弦函数的定义域和值域,点与圆的位置关系,诱导公式的应用,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目