题目内容
已知圆C:(x-3)2+(y-4)2=4
(1)若平面上有两点A(1,0),B(-1,0),点P是圆C上的动点,求使|AP|2+|BP|2取得最小值时P的坐标;
(2)若Q是x轴上的点,QM,QN分别切圆C于M,N两点,若|MN|=2
,求直线QC的方程.
(1)若平面上有两点A(1,0),B(-1,0),点P是圆C上的动点,求使|AP|2+|BP|2取得最小值时P的坐标;
(2)若Q是x轴上的点,QM,QN分别切圆C于M,N两点,若|MN|=2
| 3 |
分析:(1)设出P的坐标为(x,y),利用两点间的距离公式表示出|AP|2+|BP|2,要使|AP|2+|BP|2取得最小值只要使|OP|最小即可,由P为圆上的点,得到|OP|的最小值为|OC|-r,求出最小值,由原点O坐标与C坐标,确定出直线OC的方程,与圆方程联立组成方程组,求出方程组的解得到x与y的值,即可确定出P的坐标;
(2)设Q(x0,0),由圆的半径及弦MN的长,求出∠MCN的度数,进而确定出∠MCQ的度数,利用30度角所对的直角边等于斜边的一半求出|QC|的长,利用两点间的距离公式列出关于x0的方程,求出方程的解得到x0的值,确定出Q的坐标,即可确定出直线QC的方程.
(2)设Q(x0,0),由圆的半径及弦MN的长,求出∠MCN的度数,进而确定出∠MCQ的度数,利用30度角所对的直角边等于斜边的一半求出|QC|的长,利用两点间的距离公式列出关于x0的方程,求出方程的解得到x0的值,确定出Q的坐标,即可确定出直线QC的方程.
解答:解:(1)设P(x,y),由点A(1,0),B(-1,0),
得到|AP|2+|BP|2=(x-1)2+y2+(x+1)2+y2=2(x2+y2)+2=2|OP|2+2,
∵P为圆上的点,
∴|OP|min=|OC|-r=
-2=5-2=3,
∴(|AP|2+|BP|2)min=2×32+2=20,
此时直线OC:y=
x,
联立得:
,
解得:
或
(舍去),
∴点P的坐标为(
,
);
(2)设Q(x0,0),
∵圆C的半径r=2,|MN|=2
,
∴∠MCN=
,
又△QCN≌△QCM,∠MCQ=
,∠CMQ=
,|CM|=2,
∴|QC|=4,即(x0-3)2+(0-4)2=16,
解得:x0=3,
则所求直线QC的方程为x=3.
得到|AP|2+|BP|2=(x-1)2+y2+(x+1)2+y2=2(x2+y2)+2=2|OP|2+2,
∵P为圆上的点,
∴|OP|min=|OC|-r=
| 32+42 |
∴(|AP|2+|BP|2)min=2×32+2=20,
此时直线OC:y=
| 4 |
| 3 |
联立得:
|
解得:
|
|
∴点P的坐标为(
| 9 |
| 5 |
| 12 |
| 5 |
(2)设Q(x0,0),
∵圆C的半径r=2,|MN|=2
| 3 |
∴∠MCN=
| 2π |
| 3 |
又△QCN≌△QCM,∠MCQ=
| π |
| 3 |
| π |
| 2 |
∴|QC|=4,即(x0-3)2+(0-4)2=16,
解得:x0=3,
则所求直线QC的方程为x=3.
点评:此题考查了直线与圆的位置关系,涉及的知识有:两点间的距离公式,垂径定理,锐角三角函数定义,以及含30度直角三角形的性质,是一道综合性较强的试题.

练习册系列答案
相关题目
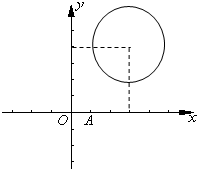 已知圆C:(x-3)2+(y-4)2=4,
已知圆C:(x-3)2+(y-4)2=4,