题目内容
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,椭圆上动点
,椭圆上动点![]() 到点
到点![]() 的最远距离和最近距离分别为
的最远距离和最近距离分别为![]() 和
和![]() .
.
(1)求椭圆的方程;
(2)设![]() 分别为椭圆的左、右顶点,过点
分别为椭圆的左、右顶点,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,若
两点,若![]() ,
,![]() 为坐标原点,求
为坐标原点,求![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据椭圆上动点![]() 到点
到点![]() 的最远距离和最近距离求得
的最远距离和最近距离求得![]() 的值,由此求得
的值,由此求得![]() 的值,结合
的值,结合![]() 求得
求得![]() 的值,进而求得椭圆方程.
的值,进而求得椭圆方程.
(2)解法一:设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和椭圆方程,写出韦达定理,结合
的方程和椭圆方程,写出韦达定理,结合![]() 求得
求得![]() 的值,然后根据三角形的面积公式求得三角形
的值,然后根据三角形的面积公式求得三角形![]() 的面积.解法二:主要步骤和解法一相同,不同点在于采用代数式恒等变换求得
的面积.解法二:主要步骤和解法一相同,不同点在于采用代数式恒等变换求得![]() 的值,其它步骤与解法一相同..
的值,其它步骤与解法一相同..
(1)设![]() ,由已知,
,由已知,![]() .∴
.∴![]() .∴
.∴![]() .则椭圆的方程为
.则椭圆的方程为![]() .
.
(2)解法1:设![]() .与椭圆联立得
.与椭圆联立得![]() .化简得
.化简得![]() .设
.设![]() ,由韦达定理,有
,由韦达定理,有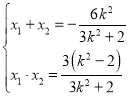 .又
.又![]() ,
,![]() .
.
![]() .
.
∴![]() .则
.则![]() .联立得
.联立得![]() .
.
则![]() .即
.即![]() .
.
∴![]() .
.
∴![]() .
.
解法2:设![]() .
.![]() ,
,
与椭圆联立得![]() .化简得
.化简得![]() .
.
其两个分别为![]() ,∴
,∴![]() .①
.①
又![]() .
.![]() .
.
∵![]() .化简得到
.化简得到![]() .②
.②
在①中,令![]() ,得
,得![]() .③
.③
令![]() ,
,![]() .∴
.∴![]() ,
,![]() .④
.④
将③、④代入②得![]() .解得
.解得![]() .
.
则![]() .即
.即![]() .
.
∴![]() .
.
∴![]() .
.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目

