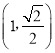题目内容
【题目】在平面直角坐标系
中，以
为极点，
轴的正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
；直线
的参数方程为
（
为参数），直线与曲线分别交于
，
两点.
（1）写出曲线的直角坐标方程和直线的普通方程；
（2）若点
的极坐标为
，
，求
的值.
【答案】(1) 曲线
的直角坐标方程为即
，直线
的普通方程为
；（2）
.
【解析】
（1）由
，得
，由此可求曲线的直角坐标方程，消去参数t可得直线的普通方程；
(2)将直线的参数方程
代入
并化简、整理，
得
. 因为直线与曲线交于
，
两点.所以
，解得
. 因为点
的直角坐标为
，在直线上，所以
即可求出
的值.
（1）由，得，
所以曲线的直角坐标方程为，
即
，
直线的普通方程为.
(2)将直线的参数方程代入并化简、整理，
得.
因为直线与曲线交于，两点。
所以
，解得.
由根与系数的关系，得
，
.
因为点的直角坐标为，在直线上.
所以
，
解得，此时满足
.且，
故.
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】某商店为了更好地规划某种商品进货的量，该商店从某一年的销售数据中，随机抽取了
组数据作为研究对象，如下表所示（
（吨）为该商品进货量，
（天）为销售天数）：
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（Ⅰ）根据上表提供的数据，求出关于的线性回归方程
；
（Ⅱ）在该商品进货量（吨）不超过
（吨）的前提下任取两个值，求该商品进货量（吨）恰有一个值不超过
（吨）的概率.
参考公式和数据：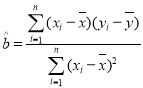
，
.
，
.
