题目内容
【题目】已知函数![]() ,
,![]() ,函数
,函数![]() 在
在![]() ,
,![]() 处取得极值,其中
处取得极值,其中![]() .
.
(1)求实数t的取值范围;
(2)判断![]() 在
在![]() 上的单调性并证明;
上的单调性并证明;
(3)已知![]() 在
在![]() 上的任意
上的任意![]() 、
、![]() ,都有
,都有![]() ,令
,令![]() ,若函数
,若函数![]() 有3个不同的零点,求实数m的取值范围.
有3个不同的零点,求实数m的取值范围.
【答案】(1)![]() ;(2)在
;(2)在![]() 上单调递增,见解析;(3)
上单调递增,见解析;(3)![]()
【解析】
(1)将问题转化为二次函数有两个不相等的正根的问题,根据一元二次方程根的分布问题求解即可;
(2)对![]() 求导,结合(1)中所求,求得导函数主导因式的正负,据此判断函数的单调性即可;
求导,结合(1)中所求,求得导函数主导因式的正负,据此判断函数的单调性即可;
(3)由题意知道![]() ,结合(1)中所求,联立
,结合(1)中所求,联立![]() 的方程组,解得
的方程组,解得![]() ,再将问题转化为
,再将问题转化为![]() 值域求解的问题,即可得到参数的范围.
值域求解的问题,即可得到参数的范围.
(1)∵![]() 有两个不等正根,
有两个不等正根,
即方程![]() 有两个不等正根a、b
有两个不等正根a、b
∴![]() 且
且![]() ,
,![]() ,
,
解得:![]() .
.
(2)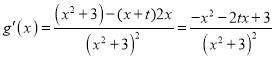 ,
,
令![]() ,则
,则![]() 的对称轴为
的对称轴为![]() .
.
∴![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
∴![]() ,于是
,于是![]() 在
在![]() 上单调递增.
上单调递增.
(3)由(2)可知:![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
即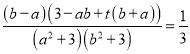
又![]() ,
,![]() ,
,![]() ,
,
解得:![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() ,
,![]() 上递增,在
上递增,在![]() 上递减
上递减
且当![]() 或
或![]() 时,
时,![]()
∴![]() 的极大值为
的极大值为![]() ,
,![]() 的极小值为
的极小值为![]() ,
,
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴当![]()
![]() 有3个不同的解,
有3个不同的解,
∴实数的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了50位高三学生的成绩进行统计分析,得到如图所示频数分布表:
分组 |
|
|
|
|
|
频数 | 3 | 11 | 18 | 12 | 6 |
(1)根据频数分布表计算成绩在![]() 的频率并计算这组数据的平均值
的频率并计算这组数据的平均值![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的学生中共抽取5人,从这5人中任取2人,求成绩在
的学生中共抽取5人,从这5人中任取2人,求成绩在![]() 和
和![]() 中各有1人的概率.
中各有1人的概率.