题目内容
已知二次函数f(x)满足f(0)=6,f(x+1)=f(x)+4x
(1)求f(x)的解析式;
(2)令g(x)=
f(|x|)+m(m∈R),若g(x)有4个零点,求m的取值范围.
(1)求f(x)的解析式;
(2)令g(x)=
| 1 |
| 2 |
考点:根的存在性及根的个数判断,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)据二次函数的形式设出f(x)的解析式,将已知条件代入,列出方程,令方程两边的对应系数相等解得.
(2)将方程的零点问题转化成函数的交点问题,作出函数的图象得到a的范围.
(2)将方程的零点问题转化成函数的交点问题,作出函数的图象得到a的范围.
解答:
 解:(1)设f(x)=ax2+bx+c,
解:(1)设f(x)=ax2+bx+c,
则f(x+1)=a(x+1)2+b(x+1)+c,f(x)+4=ax2+(b+4)x+c
∵f(0)=6;f(x+1)=f(x)+2x
∴a=2,b=-2,c=6,
∴f(x)=2x2-2x+6,
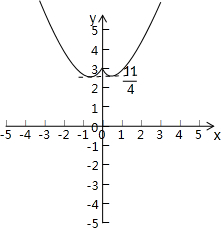
(2)依题意函数g(x)=
f(|x|)的图象与直线y=-m有4个交点.由图可知:
<-m<3
∴-3<m<-
 解:(1)设f(x)=ax2+bx+c,
解:(1)设f(x)=ax2+bx+c,则f(x+1)=a(x+1)2+b(x+1)+c,f(x)+4=ax2+(b+4)x+c
∵f(0)=6;f(x+1)=f(x)+2x
∴a=2,b=-2,c=6,
∴f(x)=2x2-2x+6,
(2)依题意函数g(x)=
| 1 |
| 2 |
| 11 |
| 4 |
∴-3<m<-
| 11 |
| 4 |
点评:本题考查利用待定系数法求函数模型已知的函数解析式,考查等价转化的能力、利用数形结合解题的数学思想方法是重点,要重视.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
把函数y=cos2x+3的图象沿向量
平移后得到函数y=sin(2x-
)的图象,则向量
是( )
| a |
| π |
| 6 |
| a |
A、(
| ||
B、(
| ||
C、(
| ||
D、(-
|
函数y=|x-1|+1的图象的对称轴方程为( )
| A、x=1 | B、x=-1 |
| C、y=1 | D、y=-1 |
 如图所示的抛物线y=-
如图所示的抛物线y=-