题目内容
 如图所示的抛物线y=-
如图所示的抛物线y=-| 1 |
| 20 |
(1)求当炮弹的射程为10千米时k值;
(2)求炮弹的射高关于k的函数g(k);
(3)问:是否存在k的值,使得通过适当调整炮弹的发射方位,就能击中飞行高度为5千米的飞行物.
考点:函数最值的应用,函数与方程的综合运用
专题:应用题,圆锥曲线的定义、性质与方程
分析:(1)由题意得:点(10,0)在抛物线上,代入可求当炮弹的射程为10千米时k值;
(2)由题意得:炮弹的射高为抛物线顶点的纵坐标,即可求炮弹的射高关于k的函数g(k);
(3)求得炮弹飞行轨迹的最大高度小于5千米,可得结论.
(2)由题意得:炮弹的射高为抛物线顶点的纵坐标,即可求炮弹的射高关于k的函数g(k);
(3)求得炮弹飞行轨迹的最大高度小于5千米,可得结论.
解答:
解:(1)由题意得:点(10,0)在抛物线上,…(2分)
∴-
(1+k2)×102+10k=0,解得:k=1.…(4分)
(2)由题意得:炮弹的射高为抛物线顶点的纵坐标,
∴g(k)=
=
(k>0).…(8分)
(3)g(k)=5(1-
),
∵k>0,∴0<
<1,∴0<g(k)<5,
∴炮弹飞行轨迹的最大高度小于5千米,
∴炮弹不可能击中飞行高度为5千米的飞行物.…(12分)
答:(1)求当炮弹的射程为10千米时k值为1;(2)炮弹的射高关于k的函数g(k)=
(k>0;(3)不存在k的值,使得通过适当调整炮弹的发射方位,就能击中飞行高度为5千米的飞行物.
∴-
| 1 |
| 20 |
(2)由题意得:炮弹的射高为抛物线顶点的纵坐标,
∴g(k)=
| -k2 | ||
4[-
|
| 5k2 |
| 1+k2 |
(3)g(k)=5(1-
| 1 |
| 1+k2 |
∵k>0,∴0<
| 1 |
| 1+k2 |
∴炮弹飞行轨迹的最大高度小于5千米,
∴炮弹不可能击中飞行高度为5千米的飞行物.…(12分)
答:(1)求当炮弹的射程为10千米时k值为1;(2)炮弹的射高关于k的函数g(k)=
| 5k2 |
| 1+k2 |
点评:本题考查函数模型的运用,考查求函数的值域,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
若m是2和8的等比中项,则椭圆x2+
=1的离心率是( )
| y2 |
| m |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
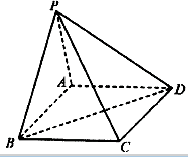 如图,在四棱锥P-ABCD中,底面ABCD是正方形,已知AB=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是正方形,已知AB=2,PA=2,PD=2