题目内容
9.已知函数f(x)=(2-a)lnx+$\frac{1}{x}$+2ax.(1)当a<0时,讨论f(x)的单调性;
(2)若对任意的a∈(-3,-2),x1,x2∈[1,3]恒有(m+ln3)a-2ln3>|f(x1)-f(x2)|成立,求实数m的取值范围.
分析 (1)求出函数的导数,求出极值点,通过两个极值点的大小,讨论函数的单调性即可.
(2)由(1)知当a∈(-3,-2)时,函数f(x)在区间[1,3]单调递减;求出x∈[1,3]时,f(x)的最值,问题等价于:对任意的a∈(-3,-2),恒有$(m+ln3)a-2ln3>1+2a-(2-a)ln3-\frac{1}{3}-6a$成立,推出不等式求解即可.
解答 解:(1)$f'(x)=\frac{2-a}{x}-\frac{1}{x^2}+2a=\frac{(2x-1)(ax+1)}{x^2}$,
令f'(x)=0,得${x_1}=\frac{1}{2}$,${x_2}=-\frac{1}{a}$,
当a=-2时,f'(x)≤0,函数f(x)在定义域(0,+∞)内单调递减;
当-2<a<0时,在区间$(0,\frac{1}{2})$,$(-\frac{1}{a},+∞)$上f'(x)<0,f(x)单调递减,
在区间$(\frac{1}{2},-\frac{1}{a})$上f'(x)>0,f(x)单调递增;
当a<-2时,在区间$(0,-\frac{1}{a})$,$(\frac{1}{2},+∞)$上f'(x)<0,f(x)单调递减,
在区间$(-\frac{1}{a},\frac{1}{2})$上f'(x)>0,f(x)单调递增.
(2)由(1)知当a∈(-3,-2)时,函数f(x)在区间[1,3]单调递减;
所以当x∈[1,3]时,f(x)max=f(1)=1+2a,$f{(x)_{min}}=f(3)=(2-a)ln3+\frac{1}{3}+6a$.
问题等价于:对任意的a∈(-3,-2),恒有$(m+ln3)a-2ln3>1+2a-(2-a)ln3-\frac{1}{3}-6a$成立,
即$am>\frac{2}{3}-4a$,因为a<0,所以$m<{(\frac{2}{3a}-4)_{min}}$,
∴实数m的取值范围为$(-∞,-\frac{13}{3}]$.
点评 本题考查函数的导数的综合应用,考查分类讨论思想以及转化思想的应用,考查分析问题解决问题的能力.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | (0,3] | B. | [-1,0) | C. | [-1,3] | D. | (3,4) |
| A. | (-$\frac{1}{2}$,0) | B. | [-$\frac{1}{2}$,0) | C. | (-∞,-$\frac{1}{2}$] | D. | (-∞,-$\frac{1}{2}$) |
| A. | [$\frac{5}{3}$,$\frac{8}{3}$] | B. | [2,$\frac{8}{3}$) | C. | [$\frac{5}{3}$,2] | D. | [$\frac{5}{3}$,2) |
| A. | $(-∞,-\frac{3}{2}]∪[-1,+∞)$ | B. | $(-∞,-\frac{5}{2}]∪[-1,+∞)$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $[-\frac{3}{2},-1]$ |
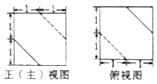 已知一个正方体截取两个全等的小正三棱锥后得到的几何体的主视图和俯视图如图,则该几何体的左视图为( )
已知一个正方体截取两个全等的小正三棱锥后得到的几何体的主视图和俯视图如图,则该几何体的左视图为( )


