题目内容
19.函数f(x)=ex,g(x)=ln(x+m)+1,(e是自然对数的底数,e≈2.71828).(Ⅰ)求函数y=f(x)的图象在点P(0,f(0))的切线l的方程;
(Ⅱ)若对任意x∈(-m,+∞),恒有f(x)≥g(x)成立,求实数m的取值范围.
分析 (Ⅰ)先求导,根据导数的几何意义即可求出切线方程,
(Ⅱ)构造函数,根据导数和函数的最值的关系,即可求出m的取值范围.
解答 解(Ⅰ)f'(x)=ex,f'(0)=1,即直线l斜率为k=1,f(0)=1,即点P(0,1).
所以直线l的方程为y=x+1.
(Ⅱ)容易证明:ex≥x+1恒成立.
设F(x)=ex-x-1,则F'(x)=ex-1,
在区间(-∞,1)上,F'(x)<0,F(x)是减函数;
在区间(0,+∞)上,F'(x)>0,F(x)是增函数.
故F(x)的最小值为F(0)=0,
即ex≥x+1恒成立.
(i)当g(x)=ln(x+m)+1≤x+1恒成立时,即m≤ex-x恒成立时,条件必然满足.
设G(x)=ex-x,则G'(x)=ex-1,在区间(-∞,1)上,G'(x)<0,G(x)是减函数,
在区间(0,+∞)上,G'(x)>0,G(x)是增函数,
即G(x)最小值为G(0)=1.
于是当m≤1时,条件满足.
(ii)当m>1时,f(0)=1,g(0)=lnm+1>1即f(0)<g(0),条件不满足.
综上所述,m的取值范围为(-∞,1].
点评 本题考查了函数的单调性、极值问题,考查函数恒成立问题,导数的应用,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知集合M={x|-2≤x≤2},N={x|y=$\sqrt{1-x}$},那么M∩N=( )
| A. | [-2,1] | B. | (-2,1) | C. | (-2,1] | D. | {-2,1} |
7.设A={x∈Z|x≤6},B={x∈Z|x>1},那么A∩B等于( )
| A. | {x|1<x≤6} | B. | {1,2,3,4,5,6} | C. | {2,3,4,5,6} | D. | {2,3,4,5} |
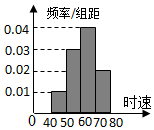 关于统计数据的分析,有以下几个结论:
关于统计数据的分析,有以下几个结论: