题目内容
以点A（-3，0），B（3，-2），C（-1，2）为顶点的三角形是（ ）
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、以上都不是 |
考点：两点间距离公式的应用
专题：直线与圆
分析：根据两点间的距离公式求出三角形的各边长度即可．
解答：
解：AB=
=
=
=2
，
BC=
=
=
=4
，
AC=
=
=2
，
∵AC2+BC2=AB2，
∴△ABC为直角三角形．
故选：C
解：AB=| (-3-3)2+22 |
| 36+4 |
| 40 |
| 10 |
BC=
| (-1-3)2+(-2-2)2 |
| 16+16 |
| 32 |
| 2 |
AC=
| (-1+3)2+22 |
| 8 |
| 2 |
∵AC2+BC2=AB2，
∴△ABC为直角三角形．
故选：C
点评：本题主要考查三角形形状的判断，利用两点间的距离公式求出长度是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在锐角△ABC中，若tanA+tanB＞0，则tanAtanB的值是（ ）
| A、大于1 |
| B、小于1 |
| C、可能等于1 |
| D、与1的关系不能确定 |
已知集合A={x|y=
}}，B={y|y=-x2+2x-1}，则A∩B=（ ）
| lg(2-x) | ||
|
| A、（-3，0] |
| B、[-3，-2] |
| C、（-∞，-3） |
| D、（-3，-2] |
直线3x+4y-9=0与圆x2+（y-1）2=1的位置关系是（ ）
| A、相离 |
| B、相切 |
| C、直线与圆相交且过圆心 |
| D、直线与圆相交但不过圆心 |
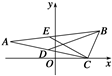如图，已知△ABC中A（-8，2），AB边上中线CE所在直线的方程为x+2y-5=0，AC边上的中线BD所在直线的方程为2x-5y+8=0，求直线BC的方程．