题目内容
1．已知{an}为等差数列，其前n项和为Sn，若a3+2a7+3a15-a17=3，则S17=$\frac{51}{5}$．分析 由已知求得a9，再由S17=17a9得答案．
解答 解：在等差数列{an}中，由a3+2a7+3a15-a17=3，
得a1+2d+2a1+12d+3a1+42d-a1-16d=3，
即5a1+40d=3，∴${a}_{1}+8d={a}_{9}=\frac{3}{5}$．
则S17=$17{a}_{9}=\frac{51}{5}$．
故答案为：$\frac{51}{5}$．
点评 本题考查等差数列的通项公式，考查等差数列的前n项和，是基础的计算题．
练习册系列答案
相关题目
17．已知sin（α+$\frac{π}{3}$）=sinα，则tanα=（ ）
| A． | $\frac{\sqrt{3}}{6}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\sqrt{3}$ |
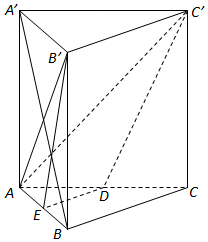如图所示，直三棱柱ABC-A′B′C中，∠ABC=90°，AB=BC=BB′=2，D为底棱AC的中点．
6．已知集合M={x|lg（x-2）≤0}，P={y|-1≤y≤3}，则M∩P=（ ）
| A． | ∅ | B． | {x|2＜x＜3} | C． | M | D． | {x|x≤3} |
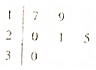某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．
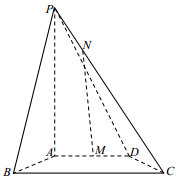如图，四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，BC=2AD=4，AB=CD，∠ABC=60°，N为线段PC上一点，CN=3NP，M为AD的中点．
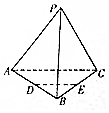如图，在正三棱锥P-ABC中，D，E分别是AB，BC的中点．