题目内容
已知sinα、sinβ是方程x2-(
cos20°)x+cos220°-
=0的两根,其中α、β都是锐角,且α>β,求α、β的度数.
| 2 |
| 1 |
| 2 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:根据题意利用韦达定理列出两个关系式,分别记作①,②,把①两边平方,利用同角三角函数间基本关系化简,将②代入得到sin2α+sin2β=1,根据题意确定出α与β的度数即可.
解答:
解:∵sinα、sinβ是方程x2-(
cos20°)x+cos220°-
=0的两根,
∴sinα+sinβ=
cos20°①,sinαsinβ=cos220°-
②,
把①两边平方得:(sinα+sinβ)2=sin2α+sin2β+2sinαsinβ=2cos220°,
将②代入得:sin2α+sin2β+2cos220°-1=2cos220°,即sin2α+sin2β=1,
∵α、β都是锐角,且α>β,
∴α+β=90°,α>β都可以成立,例如α=75°,β=15°.
| 2 |
| 1 |
| 2 |
∴sinα+sinβ=
| 2 |
| 1 |
| 2 |
把①两边平方得:(sinα+sinβ)2=sin2α+sin2β+2sinαsinβ=2cos220°,
将②代入得:sin2α+sin2β+2cos220°-1=2cos220°,即sin2α+sin2β=1,
∵α、β都是锐角,且α>β,
∴α+β=90°,α>β都可以成立,例如α=75°,β=15°.
点评:此题考查了同角三角函数间基本关系的运用,以及韦达定理,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
等差数列{an}的前n项和为Sn,若a2+a5+a8=15,a2+a4+a6=12,则S8的值是( )
| A、21 | B、24 | C、36 | D、7 |
已知集合A={1,3,4},B={1,4,6},那么A∪B=( )
| A、{2,5} |
| B、{1,3,4,6} |
| C、{1,4} |
| D、{2,3,5} |
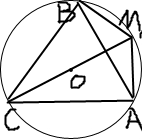 如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,a2+b2-c2=ab,CM是△ABC外接圆的直径,BM=11,AM=2,求CM的长.
如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,a2+b2-c2=ab,CM是△ABC外接圆的直径,BM=11,AM=2,求CM的长.