题目内容
14．已知命题p：x＞k，q：$\frac{3}{x+1}$≥1，若p是q的必要不充分条件，则实数k的取值范围是（ ）| A． | （2，+∞） | B． | [2，+∞） | C． | （-∞，-1） | D． | （-∞，-1] |
分析 由$\frac{3}{x+1}$≥1，化为3≥x+1，解得x范围．利用p是q的必要不充分条件，即可得出．
解答 解：由$\frac{3}{x+1}$≥1，化为3≥x+1，解得x≤2．
∵p是q的必要不充分条件，
∴k＞2．
故选：A．
点评 本题考查了简易逻辑的判定方法、不等式的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．平行直线l1：3x+4y-12=0与l2：6x+8y-15=0之间的距离为（ ）
| A． | $\frac{3}{10}$ | B． | $\frac{9}{10}$ | C． | $\frac{3}{5}$ | D． | $\frac{9}{5}$ |
5．已知函数f（x）=2cos2x+sin2x-1，则以下判断中错误的是（ ）
| A． | 函数f（x）在区间$[{\frac{π}{8}，\frac{5π}{8}}]$上是减函数 | |
| B． | 直线x=$\frac{π}{8}$是函数f（x）图象的一条对称轴 | |
| C． | 若$x∈[{0，\frac{π}{2}}]$，则函数f（x）的值域是$[{0，\sqrt{2}}]$ | |
| D． | 函数f（x）的图象可由函数y=$\sqrt{2}$sin2x的图象向左平移$\frac{π}{8}$而得到 |
2．如图为某几何体的三视图，求该几何体的内切球的表面积为（ ）
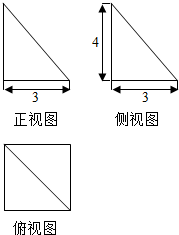
| A． | $\frac{1}{4}π$ | B． | 3π | C． | 4π | D． | $\frac{4}{3}π$ |
6．如果两个非零向量$\overrightarrow{a}$和$\overrightarrow{b}$满足等式|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|，则$\overrightarrow{a}$，$\overrightarrow{b}$应满足（ ）
| A． | $\overrightarrow{a}•\overrightarrow{b}$=0 | B． | $\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | C． | $\overrightarrow{a}•\overrightarrow{b}$=-|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | D． | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
1．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，x轴上有一点Q（2a，0），若C上存在一点P，使AP⊥PQ，则双曲线离心率的取值范围是（ ）
| A． | $e＞\frac{{\sqrt{6}}}{2}$ | B． | $1＜e＜\frac{{\sqrt{6}}}{2}$ | C． | $e≥\frac{{\sqrt{6}}}{3}$ | D． | $1＜e＜\frac{{\sqrt{6}}}{3}$ |