题目内容
6.如果两个非零向量$\overrightarrow{a}$和$\overrightarrow{b}$满足等式|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,则$\overrightarrow{a}$,$\overrightarrow{b}$应满足( )| A. | $\overrightarrow{a}•\overrightarrow{b}$=0 | B. | $\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | C. | $\overrightarrow{a}•\overrightarrow{b}$=-|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
分析 由题意可判断$\overrightarrow{a}$和$\overrightarrow{b}$方向相同,从而解得.
解答 解:∵$\overrightarrow{a}$和$\overrightarrow{b}$都是非零向量,
又∵|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,
∴$\overrightarrow{a}$和$\overrightarrow{b}$方向相同,
∴$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos0=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,
故选B.
点评 本题考查了平面向量的线性运算的应用及数量积的应用.

练习册系列答案
相关题目
16.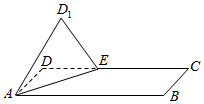 在长方形ABCD中,AD=2,AB=4,点E是边CD上的一动点,将△ADE沿直线AE翻折到△AD1E,使得二面角D1-AE-B为直二面角,则cos∠D1AB的最大值为( )
在长方形ABCD中,AD=2,AB=4,点E是边CD上的一动点,将△ADE沿直线AE翻折到△AD1E,使得二面角D1-AE-B为直二面角,则cos∠D1AB的最大值为( )
 在长方形ABCD中,AD=2,AB=4,点E是边CD上的一动点,将△ADE沿直线AE翻折到△AD1E,使得二面角D1-AE-B为直二面角,则cos∠D1AB的最大值为( )
在长方形ABCD中,AD=2,AB=4,点E是边CD上的一动点,将△ADE沿直线AE翻折到△AD1E,使得二面角D1-AE-B为直二面角,则cos∠D1AB的最大值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
14.已知命题p:x>k,q:$\frac{3}{x+1}$≥1,若p是q的必要不充分条件,则实数k的取值范围是( )
| A. | (2,+∞) | B. | [2,+∞) | C. | (-∞,-1) | D. | (-∞,-1] |
15.下列函数中是偶函数的为( )
| A. | f(x)=|x-1| | B. | f(x)=cos(x-$\frac{π}{2}$) | C. | f(x)=0 | D. | f(x)=1+x2(x≥0) |
13.命题:“?x0∈R,x02+1>0或x0>sinx0”的否定是( )
| A. | ?x∈R,x2+1≤0且x≤sinx | B. | ?x∈R,x2+1≤0或x≤sinx | ||
| C. | ?x0∈R,x${\;}_{0}^{2}$+1≤0且x0>sinx0 | D. | ?x0∈R,x${\;}_{0}^{2}$+1≤0或x0≤sinx0 |