题目内容
已知A(1,1),B(5,-2),C(3,4),O是坐标原点,P是直线OA上的一个动点
(1)求证:△ABC是钝角三角形;
(2)试确定点P的位置,使
•
取得最小值,并求此时cos∠BPC的值.
(1)求证:△ABC是钝角三角形;
(2)试确定点P的位置,使
| PB |
| PC |
考点:平面向量数量积的运算,平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:(1)利用向量的夹角公式即可判断出;
(2)利用向量共线定理和向量的夹角公式、二次函数的单调性即可得出.
(2)利用向量共线定理和向量的夹角公式、二次函数的单调性即可得出.
解答:
解:(1)∵A(1,1),B(5,-2),C(3,4),∴
=(2,3),
=(4,-3).
∴
•
=|
| |
|cos<
,
>=8-9=-1<0,
cos<
,
><0,
∴A是钝角,
∴△ABC是钝角三角形;
(2)∵P是直线OA上的一个动点,∴
=λ
=(λ,λ).
∴
•
=(5-λ,-2-λ)•(3-λ,4-λ)
=(5-λ)(3-λ)+(-2-λ)(4-λ)
=2λ2-10λ+7
=2(λ-
)2-
≥-
.
当λ=
时,使
•
取得最小值-
.
此时
=(
,
),
∴
=(
,-
),
=(
,
).
∴|
|=
,|
|=
.
∴cos∠BPC=
=
=--
.
| AC |
| AB |
∴
| AC |
| AB |
| AC |
| AB |
| AC |
| AB |
cos<
| AC |
| AB |
∴A是钝角,
∴△ABC是钝角三角形;
(2)∵P是直线OA上的一个动点,∴
| OP |
| OA |
∴
| PB |
| PC |
=(5-λ)(3-λ)+(-2-λ)(4-λ)
=2λ2-10λ+7
=2(λ-
| 5 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
当λ=
| 5 |
| 2 |
| PB |
| PC |
| 11 |
| 2 |
此时
| OP |
| 5 |
| 2 |
| 5 |
| 2 |
∴
| PB |
| 5 |
| 2 |
| 9 |
| 2 |
| PC |
| 1 |
| 2 |
| 3 |
| 2 |
∴|
| PB |
| ||
| 2 |
| PC |
| ||
| 2 |
∴cos∠BPC=
| ||||
|
|
-
| ||||||||
|
11
| ||
| 265 |
点评:本题考查了向量共线定理和向量的夹角公式、二次函数的单调性,考查了计算能力,属于中档题.

练习册系列答案
相关题目
 已知:正方形ABCD与正方形ABEF不共面,N、M分别在AE和BD上,AN=DM.
已知:正方形ABCD与正方形ABEF不共面,N、M分别在AE和BD上,AN=DM.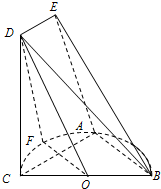 如图:已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为弧AC的中点.在梯形ACDE中,DE∥AC且AC=2DE,平面ACDE⊥平面ABC.求证:
如图:已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为弧AC的中点.在梯形ACDE中,DE∥AC且AC=2DE,平面ACDE⊥平面ABC.求证:
