题目内容
12．函数$f（x）=\frac{{\sqrt{1-x}}}{x}$的定义域为（ ）| A． | （0，1] | B． | （-∞，0） | C． | （-∞，1] | D． | （-∞，0）∪（0，1] |
分析 由根式内部的代数式大于等于0，分式的分母不等于0，列出方程组，求解即可得答案．
解答 解：由$\left\{\begin{array}{l}{1-x≥0}\\{x≠0}\end{array}\right.$，
解得：x≤1且x≠0．
∴函数$f（x）=\frac{{\sqrt{1-x}}}{x}$的定义域为：（-∞，0）∪（0，1]．
故选：D．
点评 本题考查了函数的定义域及其求法，考查了不等式的解法，是基础题．
练习册系列答案
相关题目
2．下列命题是真命题的为（ ）
| A． | ?x∈R，2x＞1 | B． | ?x∈R，x2＞0 | C． | ?x∈R，2x＜1 | D． | ?x∈R，x2＜0 |
3．函数$f（x）=\frac{{\;{2^x}}}{{\sqrt{1-x}}}+{log_3}（2x-1）$的定义域是（ ）
| A． | $（\frac{1}{2}\;，\;1）$ | B． | $[\frac{1}{2}\;，\;1）$ | C． | （1，+∞） | D． | $（\frac{1}{2}，\;1]$ |
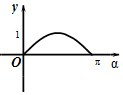
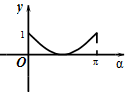
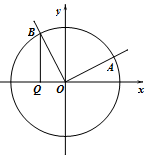如图，在平面直角坐标系xOy中，角α（0≤α≤π）的始边为x轴的非负半轴，终边与单位圆的交点为A，将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB，过点B作x轴的垂线，垂足为Q．记线段BQ的长为y，则函数y=f（α）的图象大致是（ ）
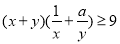对任意正实数
恒成立，则正实数
的最小值为（ ）
B．
C．
D．