题目内容
1.已知sinθ-2|cosθ|=0,且θ为第二象限的角.(1)求tanθ的值;
(2)求sin2θ-sinθ•cosθ-2cos2θ+1的值.
分析 (1)运用象限角的三角函数符号化简三角函数式,求得正切值;
(2)巧用三角函数的平方关系,将整式看作分母为1的三角函数式,化为正切的式子求值.
解答 解:(1)因为θ为第二象限的角,
所以sinθ-2|cosθ|=sinθ+2cosθ=0
得tanθ=-2,
(2)sin2θ-sinθ•cosθ-2cos2θ+1
=2sin2θ-sinθ•cosθ-cos2θ
=$\frac{{2{{sin}^2}θ-sinθ•cosθ-{{cos}^2}θ}}{{{{sin}^2}θ+{{cos}^2}θ}}$
=$\frac{{2{{tan}^2}θ-tanθ-1}}{{{{tan}^2}θ+1}}$
=$\frac{{2×{{(-2)}^2}-(-2)-1}}{{{{(-2)}^2}+1}}=\frac{9}{5}$.
点评 本题考查了化简三角函数求值以及三角函数的基本关系式的应用求值;属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.函数$f(x)=\frac{{\sqrt{1-x}}}{x}$的定义域为( )
| A. | (0,1] | B. | (-∞,0) | C. | (-∞,1] | D. | (-∞,0)∪(0,1] |
9.在极坐标系中,圆ρ=4cosθ(ρ∈R)的圆心到直线$θ=\frac{π}{3}$的距离是( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 1 | D. | 2 |
16.已知α满足sinα=$\frac{1}{3}$,那么$cos(\frac{π}{4}+α)cos(\frac{π}{4}-α)$值为( )
| A. | $\frac{25}{18}$ | B. | $-\frac{25}{18}$ | C. | $\frac{7}{18}$ | D. | $-\frac{7}{18}$ |
13.已知两点A(0,0),B(2,2)到直线l的距离分别为1和2,这样的直线l条数为( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
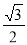 cos 2x的最小正周期和振幅分别是( )
cos 2x的最小正周期和振幅分别是( )