题目内容
17.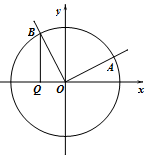 如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB,过点B作x轴的垂线,垂足为Q.记线段BQ的长为y,则函数y=f(α)的图象大致是( )
如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB,过点B作x轴的垂线,垂足为Q.记线段BQ的长为y,则函数y=f(α)的图象大致是( )| A. |  | B. |  | C. | 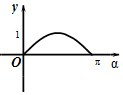 | D. | 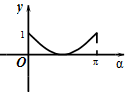 |
分析 以x轴的非负半轴为始边,OA为终边的角设为α,α∈[0,π],可得B(cos($α+\frac{π}{2}$),sin($α+\frac{π}{2}$)),即B(-sinα,cosα).记线段BQ的长为y,则函数y=f(α)=|cosα|,
解答 解:以x轴的非负半轴为始边,OA为终边的角设为α,α∈[0,π]
可得A(cosα,sinα),将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB.可得B(cos($α+\frac{π}{2}$),sin($α+\frac{π}{2}$)),
即B(-sinα,cosα).记线段BQ的长为y,则函数y=f(α)=|cosα|,
故选B.
点评 本题考查了三角函数定义的应用,考查转化思想以及计算能力,属于基础题.

练习册系列答案
相关题目
8.已知函数$f(x)=sinx+\sqrt{3}cosx$,若方程f(x)=m在闭区间[0,2π]上恰有三个解x1、x2、x3,则f(x1+x2+x3)=( )
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
12.函数$f(x)=\frac{{\sqrt{1-x}}}{x}$的定义域为( )
| A. | (0,1] | B. | (-∞,0) | C. | (-∞,1] | D. | (-∞,0)∪(0,1] |
9.在极坐标系中,圆ρ=4cosθ(ρ∈R)的圆心到直线$θ=\frac{π}{3}$的距离是( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 1 | D. | 2 |