题目内容

6．下列函数中，与函数y=2x表示同一函数的是（　　）
A．y=$\frac{2{x}^{2}}{x}$B．y=$\sqrt{4{x}^{2}}$C．y=（$\sqrt{2x}$）2D．y=log24x

分析 根据两个函数的定义域相同，对应关系也相同，即可判断它们是同一函数．

解答 解：对于A，y=$\frac{{2x}^{2}}{x}$=2x（x≠0）与y=2x（x∈R）的定义域不同，∴不是同一函数；
对于B，y=$\sqrt{{4x}^{2}}$=2|x|（x∈R）与y=2x（x∈R）的解析式不同，∴不是同一函数；
对于C，y=${（\sqrt{2x}）}^{2}$=2x（x≥0）与y=x（x∈R）的定义域不同，∴C是同一函数；
对于D，y=log24x=log222x=2x（x∈R）与y=2x（x∈R）的定义域相同，对应关系也相同，∴是同一函数．
故选：D．

点评 本题考查了判断两个函数是否为同一函数的应用问题，是基础题目．

练习册系列答案
相关题目
16．执行如图所示的程序框图后，输出的结果为（　　）
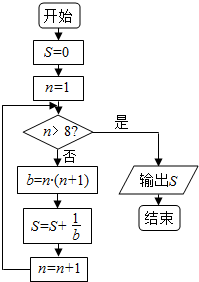
A．$\frac{7}{8}$B．$\frac{9}{10}$C．$\frac{8}{9}$D．$\frac{10}{11}$
17．函数f（x）=$\frac{2}{x}$-log3x的零点所在的一个区间是（　　）
A．（0，1）B．（1，2）C．（2，3）D．（3，4）
14．若点P（1，-1）在角φ（-π＜φ＜0）终边上，则函数y=3cos（x+φ），x∈[0，π]的单调减区间为[$\frac{π}{4}$，π]．
1．已知集合A={x|2x+a＞0}（a∈R），且1∉A，2∈A，则（　　）
A．a＞-4B．a≤-2C．-4＜a＜-2D．-4＜a≤-2
11．设$\frac{π}{2}$＜α＜π，若sin（α+$\frac{π}{6}$）=$\frac{1}{3}$，则cos（$\frac{2π}{3}$+α）=（　　）
A．-$\frac{2\sqrt{2}}{3}$B．$\frac{2\sqrt{2}}{3}$C．-$\frac{1}{3}$D．$\frac{1}{3}$
18．已知定理：“实数m，n为常数，若函数h（x）满足h（m+x）+h（m-x）=2n，则函数y=h（x）的图象关于点（m，n）成中心对称”．
（Ⅰ）已知函数f（x）=$\frac{{x}^{2}}{x-1}$的图象关于点（1，b）成中心对称，求实数b的值；
（Ⅱ）已知函数g（x）满足g（2+x）+g（-x）=4，当x∈[0，2]时，都有g（x）≤3成立，且当x∈[0，1]时，g（x）=2k（x-1）+1，求实数k的取值范围．
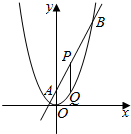15．已知抛物线C：x2=2py（p＞0）的焦点为F，直线l：y=2x+2交抛物线C于A，B两点，P是线段AB的中点，过P作x轴的垂直交抛物线C于点Q．
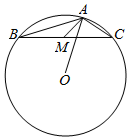（Ⅰ）若直线l过焦点F，求$\overrightarrow{AF}$•$\overrightarrow{BF}$的值；
（Ⅱ）是否存在实数p，使$\overrightarrow{AQ}$⊥$\overrightarrow{BQ}$？若存在，求出p的值；若不存在，说明理由．
16．已知△ABC外接圆的圆心为O，$AB=2\sqrt{3}$，$AC=2\sqrt{2}$，A为钝角，M是BC边的中点，则$\overrightarrow{AM}•\overrightarrow{AO}$=（　　）
A．3B．4C．5D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网