题目内容
11.已知f(x)=ax3-x2-x+b(a,b∈R,a≠0),g(x)=$\frac{{3\sqrt{e}}}{4}{e^x}$(e是自然对数的底数),f(x)的图象在x=-$\frac{1}{2}$处的切线方程为y=$\frac{3}{4}x+\frac{9}{8}$.(1)求a,b的值;
(2)探究直线y=$\frac{3}{4}x+\frac{9}{8}$.是否可以与函数g(x)的图象相切?若可以,写出切点的坐标,否则,说明理由;
(3)证明:当x∈(-∞,2]时,f(x)≤g(x).
分析 (1)求出函数的导数,根据切线方程求出a的值,求出A的坐标,得到关于b的方程,解出即可;
(2)设出切点A,根据切线方程求出A的坐标,从而求出切线方程,整理即可;
(3)问题转化为x∈(-∞,2]时,f(x)≤$\frac{3}{4}$x+$\frac{9}{8}$,令k(x)=$\frac{3}{4}$x+$\frac{9}{8}$-f(x)=-x3+x2+$\frac{7}{4}$x+$\frac{1}{2}$,根据函数的单调性证明即可.
解答 解:(1)f′(x)=3ax2-2x-1,
∵f(x)的图象在x=-$\frac{1}{2}$处的切线方程是y=$\frac{3}{4}$x+$\frac{9}{8}$,
故f′(-$\frac{1}{2}$)=$\frac{3}{4}$,即3a•${(-\frac{1}{2})}^{2}$-2•(-$\frac{1}{2}$)-1=$\frac{3}{4}$,解得:a=1;
故f(x)的图象过A(-$\frac{1}{2}$,$\frac{3}{4}$),
故${(-\frac{1}{2})}^{3}$-${(-\frac{1}{2})}^{2}$-(-$\frac{1}{2}$)+b=$\frac{3}{4}$,解得:b=$\frac{5}{8}$,
综上,a=1,b=$\frac{5}{8}$;
(2)设直线y=$\frac{3}{4}$x+$\frac{9}{8}$与函数g(x)的图象相切于A(x0,y0),
∵g′(x)=$\frac{3\sqrt{e}}{4}$ex,∴过A点的直线的斜率是g′(x0)=$\frac{3\sqrt{e}}{4}$${e}^{{x}_{0}}$,
又直线y=$\frac{3}{4}$x+$\frac{9}{8}$的斜率是$\frac{3}{4}$,故$\frac{3\sqrt{e}}{4}$${e}^{{x}_{0}}$=$\frac{3}{4}$,解得:x0=-$\frac{1}{2}$,
将x0=-$\frac{1}{2}$代入y=$\frac{3\sqrt{e}}{4}$ex得点A的坐标是(-$\frac{1}{2}$,$\frac{3}{4}$),
故切线方程为:y-$\frac{3}{4}$=$\frac{3}{4}$(x+$\frac{1}{2}$),化简得y=$\frac{3}{4}$x+$\frac{9}{8}$,
故直线y=$\frac{3}{4}$x+$\frac{9}{8}$可以与函数g(x)的图象相切,切点坐标是(-$\frac{1}{2}$,$\frac{3}{4}$);
(3)要证明:x∈(-∞,2]时,f(x)≤g(x),
只需证明x∈(-∞,2]时,f(x)≤$\frac{3}{4}$x+$\frac{9}{8}$,
令k(x)=$\frac{3}{4}$x+$\frac{9}{8}$-f(x)=-x3+x2+$\frac{7}{4}$x+$\frac{1}{2}$,
k′(x)=-3x2+2x+$\frac{7}{4}$,令k′(x)=-3x2+2x+$\frac{7}{4}$=0,
解得:x=-$\frac{1}{2}$,x=$\frac{7}{6}$,
故k(x)min=min{k(-$\frac{1}{2}$),k(2)},
∵k(-$\frac{1}{2}$)=0,k(2)=0,故k(x)min=0,
故?x∈(-∞,2],f(x)≤$\frac{3}{4}$x+$\frac{9}{8}$成立,
?x∈(-∞,2],令h(x)=g(x)-($\frac{3}{4}$x+$\frac{9}{8}$)=$\frac{3\sqrt{e}}{4}$ex-$\frac{3}{4}$x-$\frac{9}{8}$,
h′(x)=$\frac{3\sqrt{e}}{4}$ex-$\frac{3}{4}$,令h′(x)=0,x=-$\frac{1}{2}$,
x∈(-∞,-$\frac{1}{2}$)时,h′(x)<0,当x∈(-$\frac{1}{2}$,2]时,h′(x)>0,
故h(x)≥h(-$\frac{1}{2}$)=0,即?x∈(-∞,2]时,g(x)≥$\frac{3}{4}$x+$\frac{9}{8}$,
由不等式的性质的传递性得:x∈(-∞,2]时,f(x)≤g(x).
点评 本题考查了切线方程问题,考查导数的应用以及不等式的证明,是一道中档题.

 星级口算天天练系列答案
星级口算天天练系列答案| A. | [$\frac{4}{3}$,2) | B. | [$\frac{3}{4}$,2] | C. | ($\frac{3}{4}$,2) | D. | (-$∞,\frac{3}{4}$)∪(2,+∞) |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | -2 | D. | 2 |
| A. | m(1+q)4元 | B. | m(1+q)5元 | C. | $\frac{m[(1+q)^{4}-(1+q)]}{q}$元 | D. | $\frac{m[(1+q)^{5}-(1+q)]}{q}$元 |
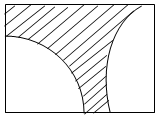 已知矩形的长为10,宽为5(如图所示),在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为560颗,则可以估计阴影部分的面积为2.8.
已知矩形的长为10,宽为5(如图所示),在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆为560颗,则可以估计阴影部分的面积为2.8. 如图,正方体ABCD-A1B1C1D1的棱长为1,M,N分别是线段A1C1和BD上的动点,则下列判断正确的是①③④⑤(把你认为正确的序号都填上)
如图,正方体ABCD-A1B1C1D1的棱长为1,M,N分别是线段A1C1和BD上的动点,则下列判断正确的是①③④⑤(把你认为正确的序号都填上)