题目内容
设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,其中an=
(1)求S1,S2,S3的值;
(2)猜出Sn的表达式,并用数学归纳法证明.
|
(1)求S1,S2,S3的值;
(2)猜出Sn的表达式,并用数学归纳法证明.
考点:数学归纳法,数列递推式
专题:综合题,点列、递归数列与数学归纳法
分析:(1)先确定Sn-1Sn-2Sn+1=0,再计算S1,S2,S3的值;
(2)由(1)猜想Sn=
,用数学归纳法证明数列问题时分为两个步骤,第一步,先证明当当n=1时,已知结论成立,第二步,先假设n=k时结论成立,利用此假设结合题设条件证明当n=k+1时,结论也成立即可.
(2)由(1)猜想Sn=
| n |
| n+1 |
解答:
解:(1)由题设(Sn-1)2-an(Sn-1)-an=0,
Sn2-2Sn+1-anSn=0.
当n≥2时,an=Sn-Sn-1,
代入上式得Sn-1Sn-2Sn+1=0.①
由(1)得S1=a1=
,S2=a1+a2=
+
=
.
由①可得S3=
.
(2)由(1)猜想Sn=
,
下面用数学归纳法证明这个结论.
(i)n=1时已知结论成立.
(ii)假设n=k时结论成立,即Sk=
,
当n=k+1时,由①得Sk+1=
,即Sk+1=
,故n=k+1时结论也成立.
综上,由(i)、(ii)可知Sn=
对所有正整数n都成立.
Sn2-2Sn+1-anSn=0.
当n≥2时,an=Sn-Sn-1,
代入上式得Sn-1Sn-2Sn+1=0.①
由(1)得S1=a1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
由①可得S3=
| 3 |
| 4 |
(2)由(1)猜想Sn=
| n |
| n+1 |
下面用数学归纳法证明这个结论.
(i)n=1时已知结论成立.
(ii)假设n=k时结论成立,即Sk=
| k |
| k+1 |
当n=k+1时,由①得Sk+1=
| 1 |
| 2-Sk |
| k+1 |
| k+2 |
综上,由(i)、(ii)可知Sn=
| n |
| n+1 |
点评:本题考查数列的函数特性,考查考查了数学归纳法,数学归纳法的基本形式:设P(n)是关于自然数n的命题,若1°P(n0)成立(奠基);2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立

练习册系列答案
相关题目
已知f(x)=log
(x2-2x)的单调递增区间是( )
| 1 |
| 2 |
| A、(1,+∞) |
| B、(2,+∞) |
| C、(-∞,0) |
| D、(-∞,1) |
已知函数y=xlnx,则这个函数在点(1,0)处的切线方程是( )
| A、y=2x-2 |
| B、y=2x+2 |
| C、y=x-1 |
| D、y=x+1 |
 曲线C1:
曲线C1: 已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,半径OC与母线PB所成的角的大小等于60°.
已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,半径OC与母线PB所成的角的大小等于60°.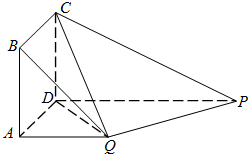 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面PDAQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面PDAQ,AB=AQ=