题目内容
3.定义域为R的奇函数f(x)=$\frac{b-h(x)}{1+h(x)}$,其中h(x)是指数函数,且h(2)=4.(1)求函数f(x)的解析式;
(2)求不等式f(2x-1)>f(x+1)的解集.
分析 (1)根据h(2)=4求得指数函数h(x)的解析式,再根据f(0)=0,求得b的值,可得f(x)的解析式.
(2)根据f(x)在R上单调递减,可得2x-1<x+1,求得x的范围.
解答 解:(1)由于h(x)是指数函数,可设h(x)=ax,a>0,a≠1,
∵h(2)=a2=4,∴a=2,∴函数f(x)=$\frac{b-h(x)}{1+h(x)}$=$\frac{b{-2}^{x}}{1{+2}^{x}}$.
∵函数f(x)=$\frac{b-h(x)}{1+h(x)}$是定义域为R的奇函数,故有f(0)=$\frac{b-1}{1+1}$=0,∴b=1,
∴f(x)=$\frac{1{-2}^{x}}{1{+2}^{x}}$.
(2)∵f(x)=$\frac{1{-2}^{x}}{1{+2}^{x}}$=$\frac{2}{{2}^{x}+1}$-1,在R上单调递减,
故由不等式f(2x-1)>f(x+1),可得2x-1<x+1,求得x<$\frac{2}{3}$,
即原不等式的解集为{x|x<$\frac{2}{3}$ }.
点评 本题主要考查用待定系数法求函数的解析式,函数的奇偶性和单调性的综合应用,属于中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
14.过两点A(4,y),B(2,-3)的直线的倾斜角为45°,则y=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -1 | D. | 1 |
11.一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )m3
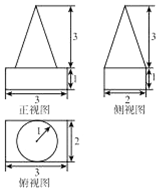

| A. | 6+π | B. | 4+π | C. | 3+π | D. | 2+π |
13.在△ABC中,角A,B,C所对的边分别为a,b,c,$\frac{π}{3}<C<\frac{π}{2}$,$\frac{b}{a-b}=\frac{sin2C}{sinA-sin2C}$,a=3,$sinB=\frac{{\sqrt{11}}}{6}$,则b等于( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $2\sqrt{3}$ |