题目内容
已知数列{an}满足a1=1,an+an-1=2n-1,n≥2,且n∈N+,则数列{
}的前n项和为( )
| an |
| 2n |
A、Sn=1-
| ||||
B、Sn=2-
| ||||
C、Sn=n(1-
| ||||
D、Sn=2-
|
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:由数列递推式结合首项求出数列前几项,猜测出数列的通项公式,利用首项归纳法证明,然后利用错位相减法求数列{
}的前n项和.
| an |
| 2n |
解答:
解:由a1=1,an+an-1=2n-1,n≥2,得
a2=2,a3=3,a4=4,…
由此猜测an=n.
下面利用首项归纳法证明:
a1=1符合;
假设n=k时成立,即ak=k,
那么,当n=k+1时,ak+1+ak=2(k+1)-1=2k+1,
则ak+1=2k+1-k=k+1,
∴当n=k+1时结论成立.
综上,an=n.
设数列{
}的前n项和为Sn.
则Sn=1•
+2•
+3•
+…+n•
①,
Sn=1•
+2•
+…+(n-1)•
+n•
②,
①-②得
Sn=
+
+…+
-
=
-
=1-
-
.
∴Sn=2-
-
.
故选:B.
a2=2,a3=3,a4=4,…
由此猜测an=n.
下面利用首项归纳法证明:
a1=1符合;
假设n=k时成立,即ak=k,
那么,当n=k+1时,ak+1+ak=2(k+1)-1=2k+1,
则ak+1=2k+1-k=k+1,
∴当n=k+1时结论成立.
综上,an=n.
设数列{
| an |
| 2n |
则Sn=1•
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
①-②得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n |
| 2n+1 |
| ||||
1-
|
| n |
| 2n+1 |
| 1 |
| 2n |
| n |
| 2n+1 |
∴Sn=2-
| 1 |
| 2n-1 |
| n |
| 2n |
故选:B.
点评:本题考查了数学归纳法证明与自然数有关的命题,考查了错位相减法求数列的和,是中档题.

练习册系列答案
相关题目
已知函数f(x)=x2+ln(x+m)与函数g(x)=x2+ex-
(x<0)的图象上存在关于y轴对称的点(e为自然对数的底数),则m的取值范围是( )
| 1 |
| 2 |
A、(-∞,
| ||||||
B、(-∞,
| ||||||
C、(-
| ||||||
D、(-
|
函数f(x)=|log2(x+1)|的图象大致是( )
A、 |
B、 |
C、 |
D、 |
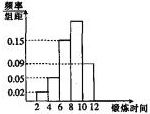 某校友200位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10]小时内的人数为( )
某校友200位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10]小时内的人数为( )| A、76 | B、82 | C、88 | D、95 |