题目内容
16.已知函数f(x)=ax3-x2+x+2,g(x)=$\frac{elnx}{x}$,若对于?x1∈(0,1],?x2∈(0,1],都有f(x1)≥g(x2),则实数a的取值范围是[-2,+∞).分析 求出g(x)的最大值,问题转化为ax3-x2+x+2≥0在(0,1]恒成立,即a≥$\frac{{x}^{2}-x-2}{{x}^{3}}$在(0,1]恒成立,令h(x)=$\frac{{x}^{2}-x-2}{{x}^{3}}$,x∈(0,1],根据函数的单调性求出a的范围即可.
解答 解:g′(x)=$\frac{e(1-lnx)}{{x}^{2}}$,而x∈(0,1],
故g′(x)>0在(0,1]恒成立,
故g(x)在(0,1]递增,
g(x)max=g(1)=0,
若?x1∈(0,1],?x2∈(0,1],使得f(x1)≥g(x2),
只需f(x)min≥g(x)max即可;
故ax3-x2+x+2≥0在(0,1]恒成立,
即a≥$\frac{{x}^{2}-x-2}{{x}^{3}}$在(0,1]恒成立,
令h(x)=$\frac{{x}^{2}-x-2}{{x}^{3}}$,x∈(0,1],
h′(x)=$\frac{-(x-1)^{2}+7}{{x}^{4}}$>0,
h(x)在(0,1]递增,
故h(x)max=h(1)=-2,
故a≥-2,
故答案为:[-2,+∞).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
12.圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则直线AB的方程是( )
| A. | x+3y=0 | B. | 3x-y=0 | C. | 3x-y-9=0 | D. | 3x+y+9=0 |
13.某地西红柿从2月1日起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/10kg)与上市时间t(单位:元)的数据如表:
(1)根据上表数据判断,函数Q=at+b,Q=at2+bt+c,Q=a•bt,Q=a•logbt中哪一个适宜作为描述西红柿种植成本Q与上市时间t的变化关系?简要说明理由;
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
| 时间t | 50 | 110 | 250 |
| 种植成本Q | 150 | 108 | 150 |
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
6.若点P(x0,y0)是曲线y=xex上任意一点,则|x0-y0-4|的最小值为( )
| A. | 4 | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 2 |
 如图,在△OAB中,$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD与BC交于点M,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.
如图,在△OAB中,$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD与BC交于点M,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.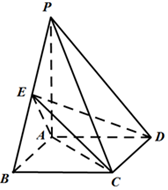 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中点.