题目内容
【题目】以平面直角坐标系中的坐标原点为极点，
轴的正半抽为极轴，建立极坐标系，曲线
的极坐标方程是
，直线
的参数方程是
（
为参数）.
（1）求曲线的直角坐标方程；
（2）若直线与曲线交于
、
两点，且
，求直线的倾斜角
.
【答案】（1）
；（2）
或
.
【解析】
（1）在曲线
的极坐标的两边同时乘以
，再由
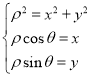，可将曲线的极坐标方程化为直角坐标方程；
（2）将直线
的参数方程代入曲线的直角坐标方程，得到关于
的一元二次方程，并列出韦达定理，借助弦长公式即可计算出
的值.
（1）在曲线的极坐标的两边同时乘以，得
，
所以，曲线的直角坐标方程为
，即；
（2）设点
、
在直线上对应的参数分别为
、
，
将直线的参数方程代入曲线的直角坐标方程，得
，
即
，
，
由韦达定理得
，
，
，得
，
，因此，
或.
练习册系列答案
名校课堂系列答案
相关题目
