题目内容
【题目】各项均为正数的数列{an}的首项
，前n项和为Sn，且Sn＋1＋Sn＝λ
..
(1)求{an}的通项公式；
(2)若数列{bn}满足bn＝λnan，求{bn}的前n项和Tn.
【答案】（1）an＝
；（2）Tn＝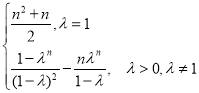
【解析】
（1）由
，得到
时，
， 两式相减得
，再由
时，得到
，即可得到数列
是首项为
，公差为的等差数列，求得其通项公式；
（2）由(1)得
，利用乘公比错位相减法，分类讨论，即可求解数列的前n项和．
（1）由题意，知，则当时，，
两式相减得，
，可得
，
因为数列的各项均为正数，所以
，且
，
所以．
当时，
，即
，
又
，所以
，所以，
故
，
所以数列是首项为，公差为的等差数列，
所以
.
（2）由(1)得
，所以
，
所以
，
，
两式相减可得
当且
时，可得
，即
；
当
时，可得
，
总上，数列
的前
项和为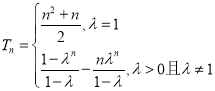
．
练习册系列答案
相关题目
