题目内容
某工厂一月份产值为50万元,采用先进技术后,第一季度共获产值182万元,二、三月份平均每月增长的百分率是多少?
解:设二、三月份平均每月增长的百分率是x,
50+50(1+x)+50(1+x)2=182,
50+50+50x+50+100x+50x2=182,
50x2+150x-32=0,
(5x+16)(5x-1)=0,
∴5x+16=0,5x-1=0,
解得x1=-3.2(负值不合题意,舍去),x2=0.2=20%.
答:二、三月份 平均每月增长的百分率是20%.
分析:等量关系为:一月份产值+一月份的产值×(1+增长率)+一月份的产值×(1+增长率)2=182,把相关数值代入计算即可.
点评:本题主要考查根据实际问题选择函数类型、一元二次方程的应用;求平均变化率的方法为:若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.
50+50(1+x)+50(1+x)2=182,
50+50+50x+50+100x+50x2=182,
50x2+150x-32=0,
(5x+16)(5x-1)=0,
∴5x+16=0,5x-1=0,
解得x1=-3.2(负值不合题意,舍去),x2=0.2=20%.
答:二、三月份 平均每月增长的百分率是20%.
分析:等量关系为:一月份产值+一月份的产值×(1+增长率)+一月份的产值×(1+增长率)2=182,把相关数值代入计算即可.
点评:本题主要考查根据实际问题选择函数类型、一元二次方程的应用;求平均变化率的方法为:若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
有一牛奶商店每瓶牛奶进价为0.80元,售价为1元,但牛奶必须于每晚进货,于次日早晨出售;昨晚进货不多可能会因供不应求减少可得利润,若进货过多,次日早晨卖不完,则不能再隔夜出售(牛奶会发酸变质),每剩一瓶则造成0.80元的损失,过去的经验可以作为未来发展的参考,历史上200天的销售记录如下:
| 日销售量 | 天数 | 概率 |
| 25瓶 | 20 | 0.10 |
| 26瓶 | 60 | 0.30 |
| 27瓶 | 100 | 0.50 |
| 28瓶 | 20 | 0.10 |
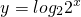 与
与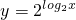
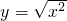 与
与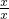
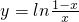
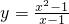
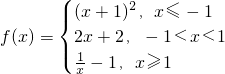 ,已知f(a)>1,则实数a的取值范围是________.
,已知f(a)>1,则实数a的取值范围是________.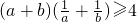

 )
) π)的值域为
π)的值域为

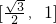
 ,其中
,其中 ,则f(x)的展开式中x4的系数为________.
,则f(x)的展开式中x4的系数为________.