题目内容
设a>0,b>0,则下列不等式中不恒成立 的是
- A.
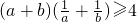
- B.|a-b|≥|a-c|-|b-c|
- C.

- D.(a+b)2≤2(a2+b2)
C
分析:根据基本不等式的性质可知. ≥
≥ 排除A,选项B:|a-b|≤|a-c|+|b-c|,所表示的含义是在三角形内两边之和大于第3边,所以显然成立.选项C不满足基本不等式的条件;看选项D时,去括号后就是基本不等式.
排除A,选项B:|a-b|≤|a-c|+|b-c|,所表示的含义是在三角形内两边之和大于第3边,所以显然成立.选项C不满足基本不等式的条件;看选项D时,去括号后就是基本不等式.
解答:∵a>0,b>0,
∴A. ≥
≥ ≥4故A恒成立,
≥4故A恒成立,
对于选项B:|a-b|≤|a-c|+|b-c|,所表示的含义是在三角形内两边之和大于第3边,所以显然成立.
C.如a,b∈R,那么a2+b2≥2ab(当且仅当a=b时取“=”号)
如果a,b是正数,
那 (当且仅当a=b时取“=”号)
(当且仅当a=b时取“=”号)
故C选项不恒成立;
D:去括号后就是基本不等式.故D恒成立.
故选C.
点评:本题主要考查了基本不等式问题.考查了学生对基础知识的掌握.要灵活运用公式,牢记公式a2+b2≥2ab成立的条件.
分析:根据基本不等式的性质可知.
 ≥
≥ 排除A,选项B:|a-b|≤|a-c|+|b-c|,所表示的含义是在三角形内两边之和大于第3边,所以显然成立.选项C不满足基本不等式的条件;看选项D时,去括号后就是基本不等式.
排除A,选项B:|a-b|≤|a-c|+|b-c|,所表示的含义是在三角形内两边之和大于第3边,所以显然成立.选项C不满足基本不等式的条件;看选项D时,去括号后就是基本不等式.解答:∵a>0,b>0,
∴A.
 ≥
≥ ≥4故A恒成立,
≥4故A恒成立,对于选项B:|a-b|≤|a-c|+|b-c|,所表示的含义是在三角形内两边之和大于第3边,所以显然成立.
C.如a,b∈R,那么a2+b2≥2ab(当且仅当a=b时取“=”号)
如果a,b是正数,
那
 (当且仅当a=b时取“=”号)
(当且仅当a=b时取“=”号)故C选项不恒成立;
D:去括号后就是基本不等式.故D恒成立.
故选C.
点评:本题主要考查了基本不等式问题.考查了学生对基础知识的掌握.要灵活运用公式,牢记公式a2+b2≥2ab成立的条件.

练习册系列答案
相关题目
设a>0,b>0,则以下不等式中不恒成立的是( )
A、(a+b)(
| ||||||
| B、a3+b3≥2ab2 | ||||||
| C、a2+b2+2≥2a+2b | ||||||
D、
|
设a>0,b>0,则以下不等式中不一定成立的是( )
A、
| ||||
| B、ln(ab+1)>0 | ||||
| C、a2+b2+2≥2a+2b | ||||
| D、a3+b3≥2ab2 |
设a>0,b>0,则下面不等式中不恒成立的是( )
A、
| ||||||||
| B、a2+b2+1>a+b | ||||||||
C、
| ||||||||
D、
|