题目内容
下列各组函数是同一函数的是
- A.
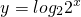 与
与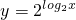
- B.
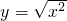 与
与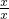
- C.y=ln(1-x)-lnx与
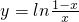
- D.y=x+1与
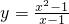
C
分析:考查各个选项中的两个函数是否具有相同的定义域、值域、对应关系,否则,便不是同一个函数.
解答:A中的两个函数的定义域不同、值域不同,所以不是同一个函数.
B中的两个函数定义域不同,故不是同一个函数.
C中,y=ln(1-x)-lnx,由 ,求得0<x<1,函数的定义域为{x|0<x<1},
,求得0<x<1,函数的定义域为{x|0<x<1},
所以函数解析式可化为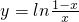 ;
;
而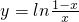 ,由
,由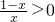 ,解得0<x<1,即函数的定义域为:{x|0<x<1},
,解得0<x<1,即函数的定义域为:{x|0<x<1},
因为两个函数的定义域与表达式相同,故是同一个函数.
D中的两个函数定义域不同,故不是同一个函数.综上,只有C中的两个函数是同一个函数.
故选 C.
点评:本题考查函数的三要素,当且仅当两个函数具有相同的定义域、值域、对应关系时,才是同一个函数.
分析:考查各个选项中的两个函数是否具有相同的定义域、值域、对应关系,否则,便不是同一个函数.
解答:A中的两个函数的定义域不同、值域不同,所以不是同一个函数.
B中的两个函数定义域不同,故不是同一个函数.
C中,y=ln(1-x)-lnx,由
 ,求得0<x<1,函数的定义域为{x|0<x<1},
,求得0<x<1,函数的定义域为{x|0<x<1},所以函数解析式可化为
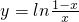 ;
;而
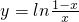 ,由
,由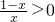 ,解得0<x<1,即函数的定义域为:{x|0<x<1},
,解得0<x<1,即函数的定义域为:{x|0<x<1},因为两个函数的定义域与表达式相同,故是同一个函数.
D中的两个函数定义域不同,故不是同一个函数.综上,只有C中的两个函数是同一个函数.
故选 C.
点评:本题考查函数的三要素,当且仅当两个函数具有相同的定义域、值域、对应关系时,才是同一个函数.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
下列各组函数是同一函数的是( )
①f(x)=
与g(x)=x
;
②f(x)=|x|与g(x)=
;
③f(x)=x0与g(x)=1;
④f(x)=x2-2x-1与g(t)=t2-2t-1.
①f(x)=
| -2x3 |
| -2x |
②f(x)=|x|与g(x)=
| x2 |
③f(x)=x0与g(x)=1;
④f(x)=x2-2x-1与g(t)=t2-2t-1.
| A、①② | B、①③ | C、②④ | D、③④ |
下列各组函数是同一函数的是( )
①f(x)=
与g(x)=x
;
②f(x)=x与g(x)=
;
③f(x)=x0与g(x)=
;
④f(x)=x2-2x-1与g(t)=t2-2t-1.
①f(x)=
| -2x3 |
| -2x |
②f(x)=x与g(x)=
| x2 |
③f(x)=x0与g(x)=
| 1 |
| x0 |
④f(x)=x2-2x-1与g(t)=t2-2t-1.