题目内容
函数y=sinx，（
π）的值域为
- A.
- B.[-1，1]
- C.
- D.
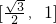
A
分析：根据正弦函数的单调区间，函数y在[
，
]上是增函数，在[，
]上是减函数，利用函数的单调性求函数的值域．
解答：由正弦函数的单调区间知，
函数y=sinx，（π）在在[，]上是增函数，在[，]上是减函数，
故x=时，y 有最大值是1，x=时，y=
，x= 时，y=
，
故函数的值域是[，1]，
故选A．
点评：本题考查正弦函数的单调区间及单调性、正弦函数的值域，利用函数的单调性求函数的值域是一种常用的方法．
分析：根据正弦函数的单调区间，函数y在[
，]上是增函数，在[，]上是减函数，利用函数的单调性求函数的值域．解答：由正弦函数的单调区间知，
函数y=sinx，（
π）在在[，]上是增函数，在[，]上是减函数，故x=
时，y 有最大值是1，x=时，y=，x= 时，y=，故函数的值域是[
，1]，故选A．
点评：本题考查正弦函数的单调区间及单调性、正弦函数的值域，利用函数的单调性求函数的值域是一种常用的方法．
练习册系列答案
相关题目
如图，已知函数y=sinx，x∈[-π，π]与x轴围成的区域记为M（图中阴影部分），若随机向圆O：x2+y2=π2内投入一米粒，则该米粒落在区域M内的概率是（ ）