题目内容
四面体ABCD的外接球为O,AD⊥平面ABC,AD=2,∠ACB=30°,AB=
,则球O的表面积为( )
| 3 |
| A、32π | ||
| B、16π | ||
| C、12π | ||
D、
|
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:由正弦定理可得△ABC外接圆的半径,利用勾股定理可得四面体ABCD的外接球的半径,即可求出球O的表面积.
解答:
解:由题意,由正弦定理可得△ABC外接圆的半径为
×
=
,
∵AD⊥平面ABC,AD=2,
∴四面体ABCD的外接球的半径为
=2,
∴球O的表面积为4π×4=16π.
故选:B.
| 1 |
| 2 |
| ||
|
| 3 |
∵AD⊥平面ABC,AD=2,
∴四面体ABCD的外接球的半径为
| 1+3 |
∴球O的表面积为4π×4=16π.
故选:B.
点评:本题考查球O的表面积,考查学生的计算能力,确定四面体ABCD的外接球的半径是关键.

练习册系列答案
相关题目
某科研所共有职工20人,其年龄统计表如下:由于电脑故障,有两个数字在表格中不能显示出来,则下列说法正确的是( )
| 年龄 | 38 | 39 | 40 | 41 | 42 |
| 人数 | 5 | 3 | 2 |
| A、年龄数据的中位数是40,众数是38 | ||
| B、年龄数据的中位数和众数一定相等 | ||
C、年龄数据的平均数
| ||
| D、年龄数据的平均数一定大于中位数 |
下列函数中,既是偶函,又在[0,1]上单调递增的是( )
| A、y=cosx |
| B、y=-x2 |
| C、y=sinxcos2x |
| D、y=|sinx| |
已知a,b,c是直线,α,β是平面,下列条件中,能得出直线a⊥平面α的是( )
| A、a⊥c,a⊥b,其中b?α,c?α |
| B、a⊥b,b∥α |
| C、α⊥β,a∥β |
| D、a∥b,b⊥α |
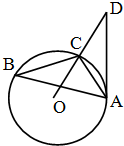 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为