题目内容
7.盒中装有10只乒乓球,其中6只新球,4只旧球,不放回地依次摸出2个球使用,在第一次摸出新球的条件下,第二次也摸出新球的概率为( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{10}$ |
分析 设事件A表示“第一次摸出新球”,事件B表示“第二次摸出新球”,分别求出P(A),P(AB),在第一次摸出新球的条件下,第二次也摸出新球的概率为:P(B|A)=$\frac{P(AB)}{P(A)}$,由此能求出结果.
解答 解:设事件A表示“第一次摸出新球”,事件B表示“第二次摸出新球”,
则P(A)=$\frac{6}{10}$=$\frac{3}{5}$,P(AB)=$\frac{6}{10}×\frac{5}{9}$=$\frac{1}{3}$,
∴在第一次摸出新球的条件下,第二次也摸出新球的概率为:
P(B|A)=$\frac{P(AB)}{P(A)}$=$\frac{\frac{1}{3}}{\frac{3}{5}}$=$\frac{5}{9}$.
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意条件概率的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD,E,F分别为PD,BC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD,E,F分别为PD,BC的中点.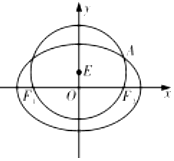 如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.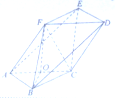 如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.
如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.