题目内容
17.在△ABC中,∠A、∠B、∠C所对边长分别为a、b、c,已知$\overrightarrow m=(sinC,sinBcosA)$,$\overrightarrow n=(b,2c)$且$\overrightarrow m•\overrightarrow n=0$.(1)求∠A的大小;
(2)若$a=2\sqrt{3}$,sinB+sinC=1,求△ABC的面积S.
分析 (1)根据$\overrightarrow m•\overrightarrow n=0$,可得bsinC+2csinBcosA=0,由正弦定理得bc+2cbcosA=0,进而得出.
(2)由(1)及余弦定理得a2=b2+c2+bc,了由正弦定理可得sin2A=sin2B+sin2C+sinBsinC,化简整理再利用三角形面积计算公式即可得出.
解答 解:(1)∵$\overrightarrow m•\overrightarrow n=0$,∴(sinC,sinBcosA)•(b,2c)=0,
∴bsinC+2csinBcosA=0…(2分)
由正弦定理得bc+2cbcosA=0…(4分)
∵b≠0,c≠0∴$cosA=-\frac{1}{2}$…(5分)
∵0<A<π∴$A=\frac{2π}{3}$…(6分)
(2)由(1)及余弦定理得a2=b2+c2+bc,
得sin2A=sin2B+sin2C+sinBsinC
即${sin^2}B+{sin^2}C+sinBsinC=\frac{3}{4}$…(8分)
又sinB+sinC=1,解得$sinB=sinC=\frac{1}{2}$…(9分)
∵$a=2\sqrt{3}$∴b=c=2…(11分)
∴△ABC的面积$S=\frac{1}{2}bcsinA=\frac{1}{2}×2×2×\frac{{\sqrt{3}}}{2}=\sqrt{3}$…(12分)
点评 本题考查了正弦定理余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.已知向量$\overrightarrow a=(1,-1),\overrightarrow b=(x,2)$,且$\overrightarrow a⊥\overrightarrow b$,则$|{\overrightarrow a+\overrightarrow b}|$的值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{7}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
6.已知三棱锥A-BCD的四个顶点A,B,C,D都在球O的表面上,BC⊥CD,AC⊥平面BCD,且AC=2$\sqrt{2}$,BC=CD=2,则球O的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 2$\sqrt{2}$π |
7.盒中装有10只乒乓球,其中6只新球,4只旧球,不放回地依次摸出2个球使用,在第一次摸出新球的条件下,第二次也摸出新球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{10}$ |
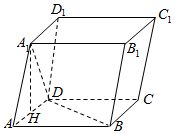 四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AD=AA1=A1D=2,H为AD中点,且A1H⊥BD.
四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AD=AA1=A1D=2,H为AD中点,且A1H⊥BD.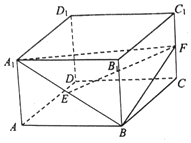 如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.
如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.