题目内容
19.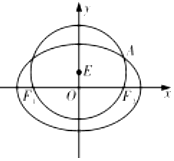 如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.(1)求椭圆C的方程;
(2)设与直线OA(O为原点)平行的直线交椭圆C于M,N两点,当△AMN的面积取取最大值时,求直线l的方程.
分析 (1)推导出F1A为圆E的直径,且|AF1|=4,从而AF2⊥F1F2.进而$c=\sqrt{3}$,再求出AF2|=2,得到a=3.由此能求出椭圆C的方程.
(2)求出点A的坐标为$(\sqrt{3},2)$,设直线l的方程为y=$\frac{2}{3}\sqrt{3}x+m$,将l方程代入$\frac{x^2}{9}+\frac{y^2}{6}=1$,得:$6{x^2}+4\sqrt{3}mx+3{m^2}-18=0$,由此利用韦达定理、根的判别式,弦长公式、点到直线距离公式,结合已知条件能求出当△AMN的面积取取最大值时,直线l的方程.
解答 解:(1)∵F1,E,A三点共线,
∴F1A为圆E的直径,且|AF1|=4,
∴AF2⊥F1F2.由x2+(0-1)2=4,得$x=±\sqrt{3}$,
∴$c=\sqrt{3}$,∵${|{A{F_2}}|^2}={|{A{F_1}}|^2}-{|{{F_1}{F_2}}|^2}=16-12=4$,
∴|AF2|=2,∴2a=|AF1|+|AF2|=6,a=3.
∵a2=b2+c2,∴b2=6,
∴椭圆C的方程为$\frac{x^2}{9}+\frac{y^2}{6}=1$.
(2)由(1)知,点A的坐标为$(\sqrt{3},2)$,
∴直线OA的斜率为$\frac{2}{3}\sqrt{3}$,故设直线l的方程为y=$\frac{2}{3}\sqrt{3}x+m$,
将l方程代入$\frac{x^2}{9}+\frac{y^2}{6}=1$消去y得:$6{x^2}+4\sqrt{3}mx+3{m^2}-18=0$,
设M(x1,y1),N(x2,y2),
∴${x_1}+{x_2}=-\frac{2}{3}\sqrt{3}m$,${x_1}{x_2}=\frac{1}{2}{m^2}-3$,△=48m2-72m2+432>0,m2<18,
∴$-3\sqrt{2}<m<3\sqrt{2}$,
又:$|{MN}|=\sqrt{1+{k^2}}|{{x_2}-{x_1}}|$=$\sqrt{1+\frac{4}{3}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{28-\frac{14}{9}{m}^{2}}$,
∵点A到直线l的距离$d=\frac{{\sqrt{21}}}{7}|m|$,
∴${S}_{△AMN}=\frac{1}{2}$|MN|•d=$\frac{1}{2}\sqrt{28-\frac{14}{9}{m}^{2}}$•$\frac{\sqrt{21}}{7}$|m|
=$\frac{\sqrt{21}}{14}$$\sqrt{(28-\frac{14}{9}{m}^{2})•{m}^{2}}$=$\frac{{\sqrt{21}}}{14}\sqrt{-\frac{14}{9}{m^4}+28{m^2}}$≤$\frac{\sqrt{21}}{14}×3\sqrt{14}$=$\frac{3}{2}\sqrt{6}$,
当且仅当${m^2}=-\frac{28}{{2×(-\frac{14}{9})}}=9$,即m=±3时等号成立,此时直线l的方程为y=$\frac{2}{3}\sqrt{3}x±3$.
点评 本题考查椭圆方程的求法、直线方程的求法,考查推理论证能力、运算求解能力,考查转化化归思想,是中档题.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | $\frac{3}{5}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{10}$ |
 当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如图:
当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如图:(1)根据茎叶图中的数据完成下面的2×2列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
| 及格(≥60) | 不及格 | 合计 | |
| 很少使用手机 | 20 | 7 | 27 |
| 经常使用手机 | 10 | 13 | 23 |
| 合计 | 30 | 20 | 50 |
参考公式及数据:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| P(K2≥K0) | 0.10 | 0.05 | 0.025 |
| K0 | 2.706 | 3.841 | 5.024 |
| A. | 1或3 | B. | -1或3 | C. | -3或1 | D. | -3或-1 |