题目内容
16.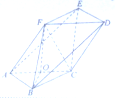 如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.
如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.(1)求证:平面ABC⊥平面ACDF;
(2)求平面AEF与平面ACE所成的锐二面角的余弦值.
分析 (1)设O是AC中点,连结OF、OB、FC,推导出OB⊥AC,OF⊥AC,则∠FOB是二面角F-AC-B的平面角,由此能证明平面ABC⊥平面ACDF.
(2)以O为原点,OB为x轴,OC为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出平面AEF与平面ACE所成的锐二面角的余弦值.
解答 证明:(1)设O是AC中点,连结OF、OB、FC,
在△ABC中,AB=BC,∴OB⊥AC,
∵四边形ACDF是菱形,∠FAC=60°,
∴△FAC是等边三角形,∴OF⊥AC,
∴∠FOB是二面角F-AC-B的平面角,
在Rt△FAO中,AF=2$\sqrt{3}$,AO=$\frac{1}{2}$AC=$\frac{1}{2}$AF=$\sqrt{3}$,
∴OF=$\sqrt{A{F}^{2}-A{O}^{2}}$=$\sqrt{6}$,
又∵BF=$\sqrt{15}$,∴OF2+OB2=BF2,
∴∠FOB=90°,
∴平面ABC⊥平面ACDF.
解:(2)由(1)知OB、OC、OF两两垂直,以O为原点,OB为x轴,OC为y轴,OF为z轴,
建立空间直角坐标系,
则A(0,-$\sqrt{3}$,0),B($\sqrt{6}$,0,0),C(0,$\sqrt{3}$,0),F(0,0,3),
$\overrightarrow{AF}$=(0,$\sqrt{3}$,3),$\overrightarrow{AC}$=(0,2$\sqrt{3}$,0),
∵AB∥DE,AF∥CD,又AB?平面CDE,AF?平面CDE,
DE?平面CDE,CD?平面CDE,
∴AB∥平面CDE,AF∥平面CDE,
又AB∩AF=A,∴平面ABF∥平面CDE,
∵EF∥BC,∴B、C、E、F四点共面,
又平面ABF∩平面BCEF=BF,平面CDE∩平面BCEF=CE,
∴BF∥CE,∴四边形BCEF是平行四边形,
∴$\overrightarrow{FE}$=$\overrightarrow{BC}$=(-$\sqrt{6},\sqrt{3}$,0),
∴$\overrightarrow{AE}=\overrightarrow{AF}+\overrightarrow{FE}$=(-$\sqrt{6},2\sqrt{3}$,3),
设平面AEF的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=\sqrt{3}y+3z=0}\\{\overrightarrow{n}•\overrightarrow{FE}=-\sqrt{6}x+\sqrt{3}y=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3},\sqrt{6},-\sqrt{2}$),
设平面ACE的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AF}=-\sqrt{6}a+2\sqrt{3}b+3c=0}\\{\overrightarrow{m}•\overrightarrow{AC}=2\sqrt{3}b=0}\end{array}\right.$,取a=$\sqrt{3}$,得$\overrightarrow{m}$=($\sqrt{3},0,\sqrt{2}$),
设平面AEF与平面ACE所成的锐二面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{55}}=\frac{\sqrt{55}}{55}$.
∴平面AEF与平面ACE所成的锐二面角的余弦值为$\frac{\sqrt{55}}{55}$.
点评 本题考查直线与直线、直线与平面、平面与平面的位置关系以及二面角等基础知识,考查空间想象能力,推理论证能力、运算求解能力,考查化归与转化思想,数形结合思想、函数与方程思想,是中档题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | 4π | B. | 8π | C. | 16π | D. | 2$\sqrt{2}$π |
| A. | $\frac{3}{5}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{10}$ |
 当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如图:
当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如图:(1)根据茎叶图中的数据完成下面的2×2列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
| 及格(≥60) | 不及格 | 合计 | |
| 很少使用手机 | 20 | 7 | 27 |
| 经常使用手机 | 10 | 13 | 23 |
| 合计 | 30 | 20 | 50 |
参考公式及数据:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| P(K2≥K0) | 0.10 | 0.05 | 0.025 |
| K0 | 2.706 | 3.841 | 5.024 |
| A. | {0,1} | B. | {-1,0,1} | C. | ∅ | D. | {-1} |
| A. | 21 | B. | -21 | C. | 441 | D. | -441 |