题目内容
函数f(x)=
的定义域为 .
log
|
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:要使函数有意义,则需2-x>0,且log
(2-x)≥0,运用对数函数的单调性,即可得到定义域.
| 1 |
| 2 |
解答:
解:要使函数有意义,则需
2-x>0,且log
(2-x)≥0,
即有x<2,且log
(2-x)≥log
1,
解得,1≤x<2.
则定义域为[1,2),
故答案为:[1,2).
2-x>0,且log
| 1 |
| 2 |
即有x<2,且log
| 1 |
| 2 |
| 1 |
| 2 |
解得,1≤x<2.
则定义域为[1,2),
故答案为:[1,2).
点评:本题考查函数的定义域的求法,注意偶次根式被开方式非负,对数的真数大于0,属于基础题.

练习册系列答案
相关题目
若(x2+ax+1)6(a>0)的展开式中x2的系数是66,则
sinxdx的值为( )
| ∫ | a 0 |
| A、1+cos2 |
| B、1-sin2 |
| C、1-cos2 |
| D、1+sin2 |
集合A={(x,y)|y=x},集合B={(x,y)|
}之间的关系是( )
|
| A、A∈B | B、B∈A |
| C、A⊆B | D、B⊆A |
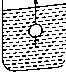 如图所示,在一个盛满水的圆柱形容器内的水面下有一个用细绳吊着的薄壁小球,小球下方有一个小孔,当慢慢地、均匀地将小球从水下面往上拉动时,圆柱形容器内水面的高度h与时间t的函数关系图象大致为( )
如图所示,在一个盛满水的圆柱形容器内的水面下有一个用细绳吊着的薄壁小球,小球下方有一个小孔,当慢慢地、均匀地将小球从水下面往上拉动时,圆柱形容器内水面的高度h与时间t的函数关系图象大致为( )A、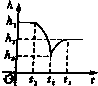 |
B、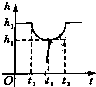 |
C、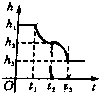 |
D、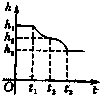 |
已知向量
,
不共线,若
=λ1
+
,
=
+λ2
,则“A、B、C三点共线”是“λ1λ2=1”的( )
| a |
| b |
| AB |
| a |
| b |
| AC |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设x,y∈R,则“x+y>2”是“x,y中至少有一个数大于1”成立的.
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |