题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 存在两个零点
存在两个零点![]() ,
,![]() ,使
,使![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;(2)2.
单调递减;(2)2.
【解析】
(1)对函数求导![]() ,由x>0,进而对
,由x>0,进而对![]() 和
和![]() 分别讨论,得出
分别讨论,得出![]() 的单调性.(2)函数
的单调性.(2)函数![]() 有两个零点
有两个零点![]() ,
,![]() ,得
,得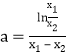 ,代入
,代入![]() ,令
,令![]() ,则
,则![]() ,设
,设![]() ,求导得
,求导得![]() 在
在![]() 上的最值即可.
上的最值即可.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
(2)因为![]() ,
,![]() ,即
,即![]() ,
,![]() .
.
两式相减得![]() ,即
,即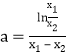 .
.
由已知![]() ,得
,得![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,即
,即 .
.
不妨设![]() ,则有
,则有![]() .
.
令![]() ,则
,则![]() ,所以
,所以![]() ,即
,即![]() 恒成立.
恒成立.
设![]() .
.
![]() .
.
令![]() ,
,![]() ,
,![]() 的图象开口向上,对称轴方程为
的图象开口向上,对称轴方程为![]() ,
,
方程![]() 的判别式
的判别式![]() .
.
当![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,![]() ,所以
,所以![]() ,
,
![]() 在
在![]() 单调递增,所以
单调递增,所以![]() 在
在![]() 恒成立.
恒成立.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,
,
![]() 在
在![]() 单调递增,所以
单调递增,所以![]() 在
在![]() 恒成立.
恒成立.
当![]() 时,
时,![]() 在
在![]() 单调递减,因为
单调递减,因为![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]()
当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
当![]() 时,都有
时,都有![]() ,
,
所以![]() 在
在![]() 不恒成立.
不恒成立.
综上所述,![]() 的取值范围是
的取值范围是![]() ,所以
,所以![]() 的最大值为2.
的最大值为2.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数 | 未损坏餐椅数 | 总计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总计 | 80 | 320 | 400 |
![]() 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
![]() 请说明是否有
请说明是否有![]() 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神
有关?![]() 参考公式:
参考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|