Question

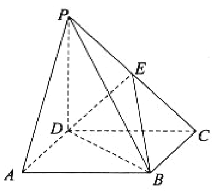
【题目】如图，在四棱锥中，底面是平行四边形，平面，，，是棱上的一点.

（1）证明：平面；

（2）若平面，求的值；

（3）在（2）的条件下，三棱锥的体积是18，求点到平面的距离.

Answer 1

【答案】（1）见解析 ；（2） ；（3）.

【解析】

（1）推导出BC⊥PD，BD⊥BC，由此能证明BC⊥平面PBD．（2）连结AC，交BD于O，连结OE，由PA∥平面BDE，得OE∥PA，由此能求出 ．（3）B到平面PCD的距离d＝

3，设PD＝a，则 ＝ ，由三棱锥P﹣BDE的体积是18，求出PD＝a＝6，设点D到平面PAB的距离为h，由VP﹣ABD＝VD﹣PAB，能求出D点到平面PAB的距离．

（1）∵在四棱锥P﹣ABCD中，底面ABCD是平行四边形，PD⊥平面ABCD，

∴BC⊥PD，∵AD＝BD＝6，AB＝6，BC＝AD，∴BD2+BC2＝CD2，∴BD⊥BC，

∵PD∩BD＝D，∴BC⊥平面PBD．

（2）连结AC交BD于O，连结OE，则O是AC的中点，

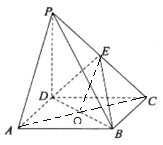
∵PA∥平面BDE，∴OE∥PA，∴E是PC的中点，∴＝．

（3）B到平面PCD的距离d＝＝3，设PD＝a，则＝＝，∵三棱锥P﹣BDE的体积是18，∴VP﹣BDE＝VB﹣PDE＝＝＝18，解得PD＝a＝6，设点D到平面PAB的距离为h，

∵PD⊥平面ABCD，AD＝BD＝6，AB＝6，

∴PA＝PB＝＝6，

∴＝18，

＝＝18，

∵VP﹣ABD＝VD﹣PAB，∴，

∴h＝＝＝2．∴D点到平面PAB的距离为2．