题目内容
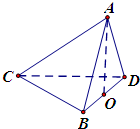 如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=
如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=| 2 |
(1)求证:AO⊥平面BCD;
(2)求异面直线AB与CD所成角的余弦值.
考点:直线与平面垂直的判定,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)求出AC,连结CO,证明AO⊥CO,然后利用直线与平面垂直的判定定理证明AO⊥平面BCD.
(2)分别取BC、AC的中点E、F,连结EF、EG,说明∠FEO或其补角就是异面直线AB、CD所成的角,连结FO,在△EFO中,求解cos∠FEO即可.
(2)分别取BC、AC的中点E、F,连结EF、EG,说明∠FEO或其补角就是异面直线AB、CD所成的角,连结FO,在△EFO中,求解cos∠FEO即可.
解答:
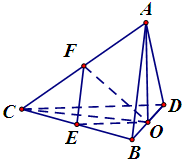 解:(1)证明:在三角形ABC中,因为AB=AD=
解:(1)证明:在三角形ABC中,因为AB=AD=
,O是BD中点,
所以AO⊥BD,且AC=
=1------------------(2分)
连结CO,在等边三角形BCD中易得CO=
,
所以AC2=22=12+(
)2=AO2+CO2,
所以AO⊥CO--------------------------------(4分)
因为CO∩BD=O,CO、BD?平面BCD
所以AO⊥平面BCD---------------------(6分)
(2)分别取BC、AC的中点E、F,连结EF、EG
因为EF
AB,EO
CD
所以∠FEO或其补角就是异面直线AB、CD所成的角---------(8分)
连结FO,因为AO⊥平面BCD,所以AO⊥CO,
所以在Rt△ACO中,斜边AC上的中线FO=
AC=1,
又因为EO=
CD=1,EF=
AB=
,
所以在△EFO中,cos∠FEO=
=
因为cos∠FEO>0,所以异面直线AB、CD所成的角的余弦值是
-------------------(14分)
 解:(1)证明:在三角形ABC中,因为AB=AD=
解:(1)证明:在三角形ABC中,因为AB=AD=| 2 |
所以AO⊥BD,且AC=
(
|
连结CO,在等边三角形BCD中易得CO=
| 3 |
所以AC2=22=12+(
| 3 |
所以AO⊥CO--------------------------------(4分)
因为CO∩BD=O,CO、BD?平面BCD
所以AO⊥平面BCD---------------------(6分)
(2)分别取BC、AC的中点E、F,连结EF、EG
因为EF
| ∥ |
. |
| ∥ |
. |
| 1 |
| 2 |
所以∠FEO或其补角就是异面直线AB、CD所成的角---------(8分)
连结FO,因为AO⊥平面BCD,所以AO⊥CO,
所以在Rt△ACO中,斜边AC上的中线FO=
| 1 |
| 2 |
又因为EO=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
所以在△EFO中,cos∠FEO=
| EF2+EO2-FO2 |
| 2EF•EO |
| ||
| 4 |
因为cos∠FEO>0,所以异面直线AB、CD所成的角的余弦值是
| ||
| 4 |
点评:本题列出直线与垂直的判定定理的应用,异面直线所成角的求法,考查转化思想的应用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
已知圆台的上下底面半径分别为1和2,高为1,则该圆台的全面积为( )
A、3
| ||||
B、(5+3
| ||||
C、
| ||||
D、
|
(文数)已知函数y=tanwx在(-
,
)内是增函数,则( )
| π |
| 2 |
| π |
| 2 |
| A、0<w≤1 | B、-1≤w<0 |
| C、w≥1 | D、w≤-1 |
直线x-y=0被圆x2+y2=1截得的弦长为( )
| A、2 | B、1 | C、4 | D、3 |
为了得到函数y=sin
x的图象,只需把函数y=sinx图象上所有的点的( )
| 1 |
| 3 |
| A、横坐标伸长到原来的3倍,纵坐标不变 | ||
B、横坐标缩小到原来的
| ||
| C、纵坐标伸长到原来的3倍,横坐标不变 | ||
D、纵坐标伸长到原来的
|
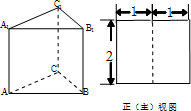 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )