题目内容
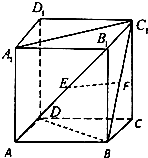
1. 如图所示,斜三棱柱ABC-A1B1C1中,点D,D1分别为AC,A1C1上的中点.
如图所示,斜三棱柱ABC-A1B1C1中,点D,D1分别为AC,A1C1上的中点.(1)证明AD1∥平面BDC1;
(2)证明BD∥平面AB1D1.
分析 (1)根据四边形ACC1A1为平行四边形可得AD1∥DC1,故而AD1∥平面BDC1;
(2)由平行四边形的性质得出DD1,AA1,BB1平行且相等,故而四边形DBB1D1是平行四边形,于是B1D1∥BD,从而得出BD∥平面AB1D1.
解答  证明:(1)∵AC$\stackrel{∥}{=}$A1C1,D,D1分别是AC,A1C1上的中点,
证明:(1)∵AC$\stackrel{∥}{=}$A1C1,D,D1分别是AC,A1C1上的中点,
∴AD$\stackrel{∥}{=}$C1D1,
∴四边形ADC1D1是平行四边形,
∴AD1∥DC1,
又AD1?平面BDC1,DC1?平面BDC1,
∴AD1∥平面BDC1.
(2)连结DD1,
∵四边形ACC1A1是平行四边形,D,D1分别是AC,A1C1上的中点,
∴DD1$\stackrel{∥}{=}A{A}_{1}$,又AA1$\stackrel{∥}{=}$BB1,
∴DD1$\stackrel{∥}{=}$BB1,
∴四边形DBB1D1是平行四边形,
∴B1D1∥BD,
又BD?平面AB1D1,B1D1?平面AB1D1.,
∴BD∥平面AB1D1.
点评 本题考查了线面平行的判定,寻找平行线是证明此类问题的关键,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
9.已知集合A={x|(x2-5x+6)(x2-12x+35)=0},集合B是元素小于10的质数,则集合A与B的关系为( )
| A. | A=B | B. | A?B | C. | B?A | D. | A?B |
13.研究表明,成年人的身高和体重具有线性相关性.小明随机调查了五名成年人甲乙丙丁戊的身高和体重,得到的结果如下表所示,根据表格中数据回答下列问题.
(1)从这五名成年人中任选两名做问卷调查,求选出的两名成年人的身高超过了170cm且体重均超过60kg的概率;
(2)求身高x与体重y的回归直线方程y=bx+a,并据此推测身高为180cm的成年人的体重大约是多少?
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| 身高x(cm) | 166 | 170 | 172 | 174 | 178 |
| 体重y(kg) | 55 | 60 | 65 | 65 | 70 |
(2)求身高x与体重y的回归直线方程y=bx+a,并据此推测身高为180cm的成年人的体重大约是多少?